当前位置： 首页 > article >正文

前缀和 及其优化技巧Ⅱ

article 2024/12/25 21:14:50

 

一. 前缀和的简单介绍

1.前缀和的数组型简单定义

        对于数组nums来说，前缀和pre[i] = pre[i-1] + nums[i]，即每个位置上存储的是前i个数组元素的和，用数学公式表示为：

pre[i] = \sum_{j=0}^{j=i}nums[j]

数组的典型案例：

其他类型的前缀和多是最终能变成和数量相关，即转换成int[] 数组类型。

那么，对于后缀和是一样的道理。

2.前缀和的典型使用场景/触发关键词

        在一些题目或者场景中，出现了子数组*，连续一段区间，并且和求数量或者判断数量相关，很大程度上可以向前缀和的方去思考。

二. 使用前缀和的经典案例 

1.leetcode1413 逐步求和得到正数的最小值

见 前缀和 及其优化技巧

2.leetcode2383 赢得比赛需要的最少训练时长

见 前缀和 及其优化技巧

3.leetcode2389 和有限的最长子序列

给你一个长度为 n 的整数数组 nums ，和一个长度为 m 的整数数组 queries 。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是 nums 中 元素之和小于等于 queries[i] 的 子序列 的 最大 长度  。

子序列 是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：
- 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
- 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
- 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。
class Solution {
    public int[] answerQueries(int[] nums, int[] queries) {
        int[] pre = new int[nums.length];
        Arrays.sort(nums);
        pre[0] = nums[0];
        for(int i = 1; i < nums.length; i++){
            pre[i] = pre[i-1] + nums[i];
        }
        int[] ans = new int[queries.length];
        for(int i = 0; i < queries.length; i++){
            int len = find(pre,queries[i]);
            ans[i] = len;
        }
        return ans;
    }
    public int find(int[] pre, int target){
        return erfen(pre,target,0,pre.length-1);
    }
    public int erfen(int[] pre, int target, int left, int right){
        if(left <= right){
            int mid = left + ((right-left)>>1);
            if(pre[mid] > target){
                return erfen(pre,target,left,mid-1);
            }
            else if(pre[mid] < target){
                return erfen(pre,target,mid+1,right);
            }
            else{
                return mid+1;
            }
        }
        return right+1;
    }
}

本题小结：（1）此题运用基础前缀和，不需要做其他变换

                  （2）在查找方面需要用二分，否则时间复杂度很高，若有较长判例会超过时间复杂度
 

4.leetcode560 和为 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数 。

输入：nums = [1,1,1], k = 2
输出：2
class Solution {
    public int subarraySum(int[] nums, int k) {
        int len = nums.length;
        int count = 0;
        int[] presum = new int[len+1];
        presum[0] = 0;
        for(int i = 0; i < len; i++){
            presum[i+1] += presum[i]+nums[i]; 
        }
        for(int left = 0; left < len; left++){
            for(int right = left+1; right <= len; right++){
                if(presum[right] - presum[left] == k){
                    count++;
                }
            }
        }
        return count;
    }
}

本题小结：（1）此题运用基础前缀和

                  （2）此题也可以进行优化，即先得到前缀和，然后用HashMap存储，再次遍历找HashMap中是否有k-pre[i]，思想类似于两数之和，在前篇前缀和 及其优化技巧 已经见的非常多了

三. 前缀和优化

1.leetcode1871 跳跃游戏 VII(前缀和+动态规划)

2.leetcode1590 使数组和能被 P 整除(前缀和+HashMap)

3.面试题 17.05.  字母与数字(前缀和+HashMap)

1~3 见 前缀和 及其优化技巧

4.leetcode209 长度最小的子数组(前缀和+二分/滑动窗口)

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

（1）前缀和

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int[] pre = new int[nums.length+1];
        pre[1] = nums[0];
        int min = nums.length;
        if(nums[0] >= target) return 1;
        for(int i = 2; i < nums.length+1; i++){
            pre[i] = pre[i-1] + nums[i-1];
        }
        if(pre[nums.length] < target) return 0;
        for(int i = 1; i < nums.length+1; i++){
            for(int j = 0; j < i; j++){
                if(pre[i] - pre[j] >= target){
                    min = Math.min(min,i-j);
                }
            }
        }
        return min;
    }
}

最基础前缀和，不再赘述，此解法不能AC，时间复杂度O(n^2)

本题小结：（1） int[] pre = new int[nums.length+1]前缀和的长度比数组长一些利于后续操作，是前缀和中经常使用的操作。

（2）前缀和剪枝

在最基础的前缀和上，可以进行剪枝

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int[] pre = new int[nums.length+1];
        pre[1] = nums[0];
        int min = nums.length;
        if(nums[0] >= target) return 1;
        for(int i = 2; i < nums.length+1; i++){
            pre[i] = pre[i-1] + nums[i-1];
        }
        if(pre[nums.length] < target) return 0;
        for(int i = 1; i < nums.length+1; i++){
            for(int j = i-1; j >= 0; j--){
                if(pre[i] < target) break;
                if(pre[i] - pre[j] >= target){
                    min = Math.min(min,i-j);
                    break;
                }
            }
        }
        return min;
    }
}

 可以通过，时间较长

剪枝（1）当在i处前缀和<target,证明在当前长度的子数组之和<target,可直接跳过

       （2）当在j处有一个结果使得pre[i] - pre[j] >= target，直接break，因为再往前长度更长，结果不可能比当前j处小

（3）前缀和+二分

前缀和天然具有二分性质，在leetcode2389 和有限的最长子序列中利用的也是这一点

对于本题可以在构建好前缀和后，使用二分【1】

class Solution {
    public int minSubArrayLen(int t, int[] nums) {
        int n = nums.length, ans = n + 10;
        int[] sum = new int[n + 10];
        for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + nums[i - 1];
        for (int i = 1; i <= n; i++) {
            int s = sum[i], d = s - t;
            int l = 0, r = i;
            while (l < r) {
                int mid = l + r + 1 >> 1;
                if (sum[mid] <= d) l = mid;
                else r = mid - 1;
            }
            if (sum[r] <= d) ans = Math.min(ans, i - r);
        }
        return ans == n + 10 ? 0 : ans;
    }
}

（4）滑动窗口【3】

对于子数组的题目来说，滑动窗口也是经常使用的方法，在前缀和的题目中可以多考虑滑动窗口，实际上，此题在时间和空间复杂度上更适合用滑动窗来解决。

class Solution {
    public int minSubArrayLen(int s, int[] nums) {
        int n = nums.length;
        if (n == 0) {
            return 0;
        }
        int ans = Integer.MAX_VALUE;
        int start = 0, end = 0;
        int sum = 0;
        while (end < n) {
            sum += nums[end];
            while (sum >= s) {
                ans = Math.min(ans, end - start + 1);
                sum -= nums[start];
                start++;
            }
            end++;
        }
        return ans == Integer.MAX_VALUE ? 0 : ans;
    }
}

5.2488 统计中位数为 K 的子数组(前缀和+HashMap/数组)

给你一个长度为 n 的数组 nums ，该数组由从 1 到 n 的 不同 整数组成。另给你一个正整数 k 。

统计并返回 nums 中的 中位数 等于 k 的非空子数组的数目。

注意：

数组的中位数是按 递增 顺序排列后位于 中间 的那个元素，如果数组长度为偶数，则中位数是位于中间靠 左 的那个元素。
例如，[2,3,1,4] 的中位数是 2 ，[8,4,3,5,1] 的中位数是 4 。
子数组是数组中的一个连续部分。

输入：nums = [3,2,1,4,5], k = 4
输出：3
解释：中位数等于 4 的子数组有：[4]、[4,5] 和 [1,4,5] 。

（1）前缀和+HashMap

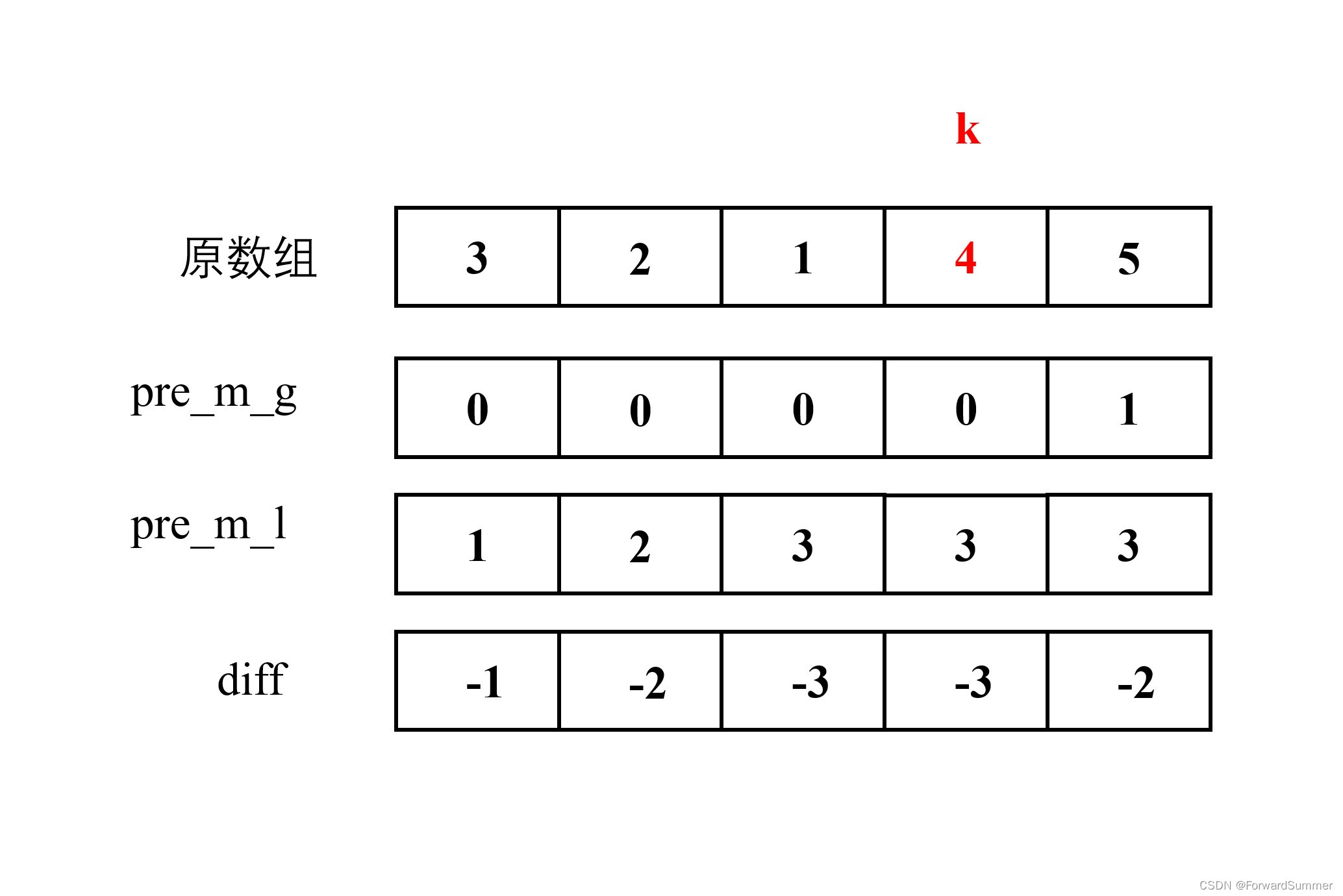
老朋友，直接上图理解

以nums = [3,2,1,4,5], k = 4为例： 

class Solution {
    public int countSubarrays(int[] nums, int k) {
        HashMap<Integer,Integer> map = new HashMap<>();
        map.put(0,1);
        int index = 0;
        int pre_m_g = 0;
        int pre_m_l = 0;
        int ans = 0;
        for(int i = 0; i < nums.length; i++){
            if(nums[i] == k){
                index = i;
                break;
            }
            if(nums[i] > k) pre_m_g++;
            if(nums[i] < k) pre_m_l++;
            int diff = pre_m_g - pre_m_l;
            if(map.containsKey(diff)){
                map.put(diff,map.get(diff)+1);
            }
            else{
                map.put(diff,1);
            }
        }
        for(int i = index; i < nums.length; i++){
            if(nums[i] > k) pre_m_g++;
            if(nums[i] < k) pre_m_l++;
            int diff = pre_m_g-pre_m_l;
            if(map.containsKey(diff)){
                ans += map.get(diff);
            }
            if(map.containsKey(diff-1)){
                ans += map.get(diff-1);
            }
        }
        return ans;
    }
}

（2）类前缀和遍历+数组

上方用HashMap的方法比较好理解，用类似的思想，采用数组映射的方式【2】

class Solution {
    public int countSubarrays(int[] nums, int k) {
        int n = nums.length;
        int i = 0;
        for (; nums[i] != k; ++i) {}
        int[] cnt = new int[n << 1 | 1];
        int ans = 1;
        int x = 0;
        for (int j = i + 1; j < n; ++j) {
            x += nums[j] > k ? 1 : -1;
            if (x >= 0 && x <= 1) {
                ++ans;
            }
            ++cnt[x + n];
        }
        x = 0;
        for (int j = i - 1; j >= 0; --j) {
            x += nums[j] > k ? 1 : -1;
            if (x >= 0 && x <= 1) {
                ++ans;
            }
            ans += cnt[-x + n] + cnt[-x + 1 + n];
        }
        return ans;
    }
}

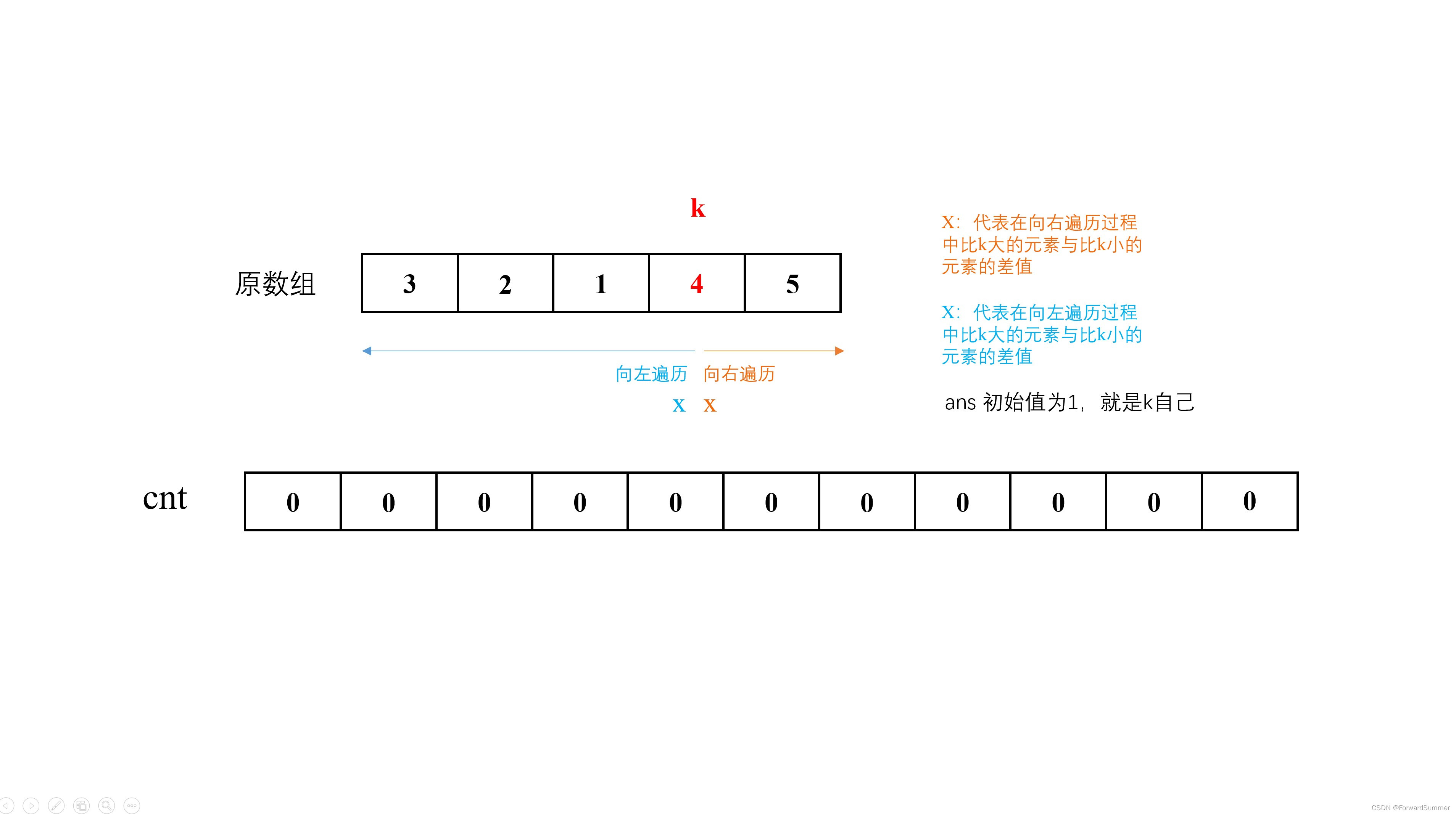
【2】：“在编码上，我们可以直接开一个长度为2*n+1的数组，用于统计当前数组中，比k大的个数和比k小的个数的差值，加上n即可把范围从[-n,n]传换成[0,2n]” 

不好理解，上图：

（1）###

（2） ###

 

（3）###

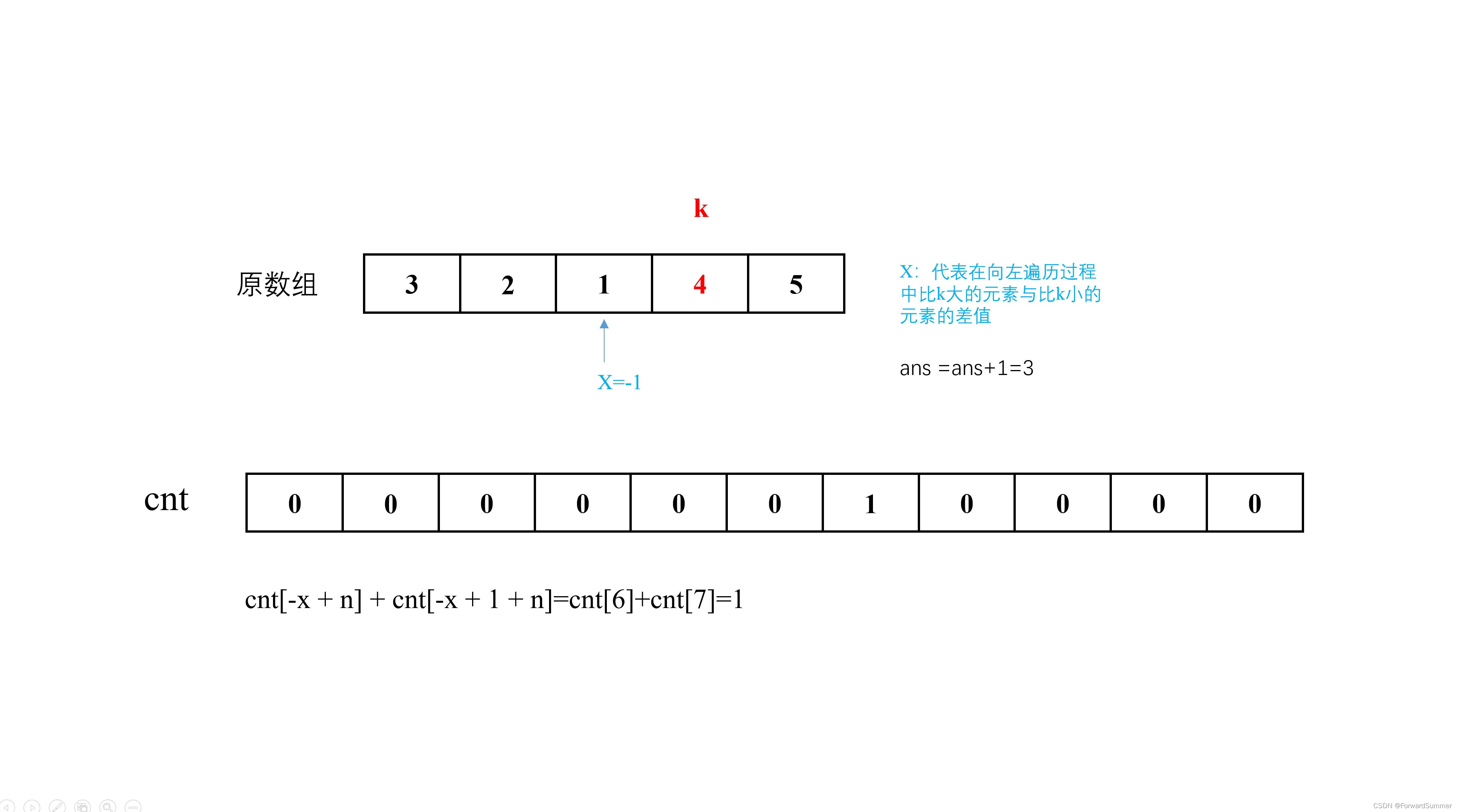
（4）###

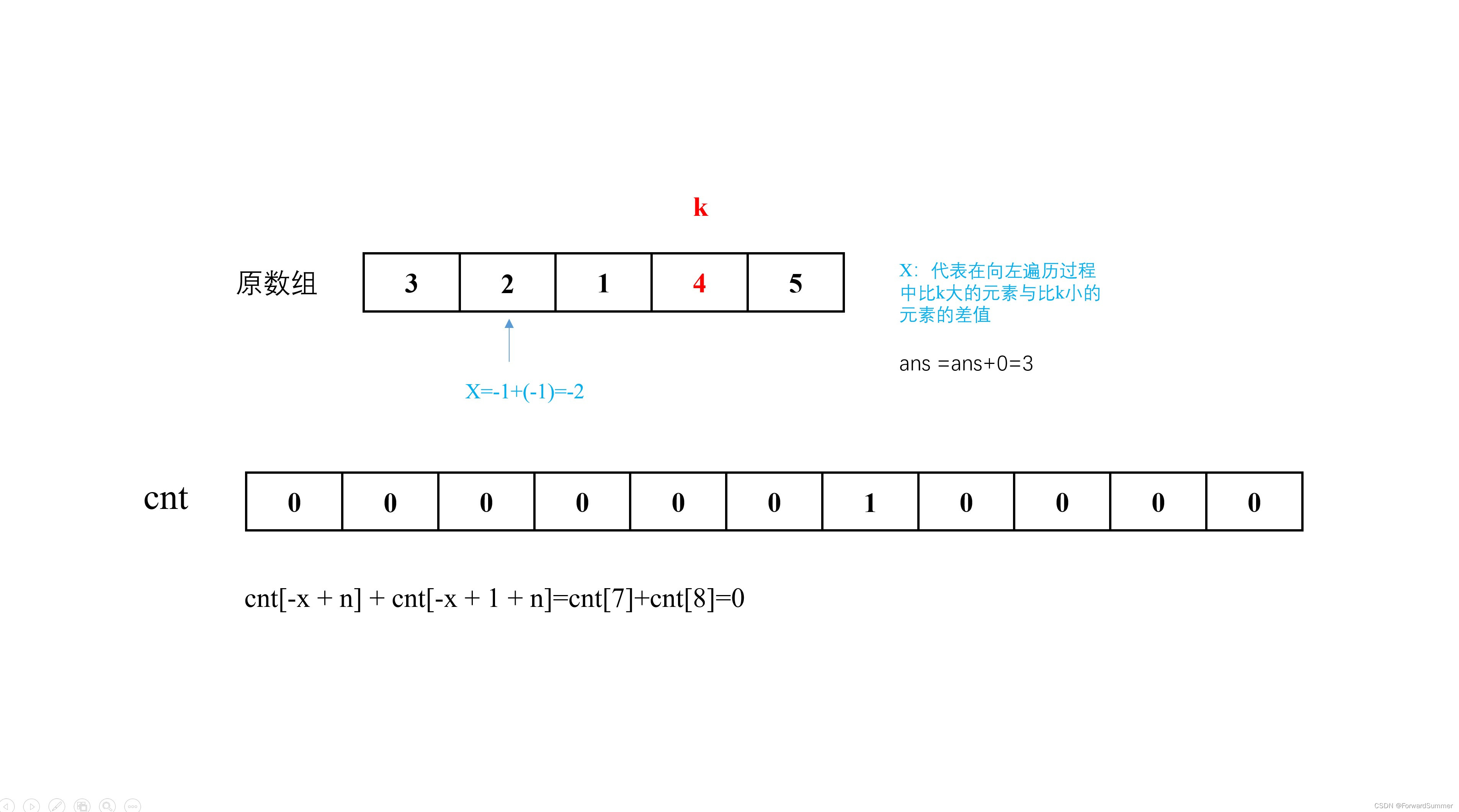
（5）###

（6）###

 

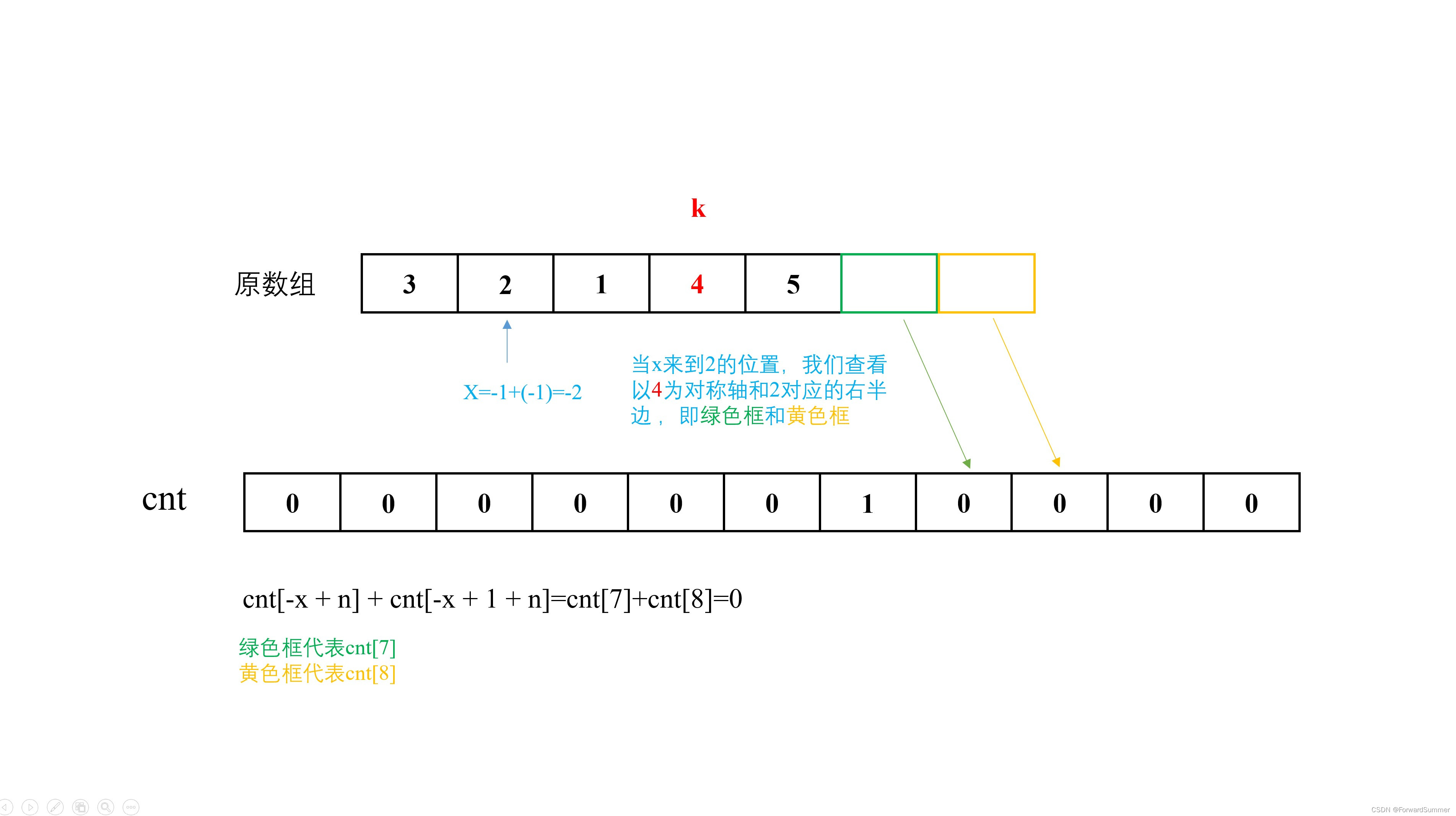
（7）###

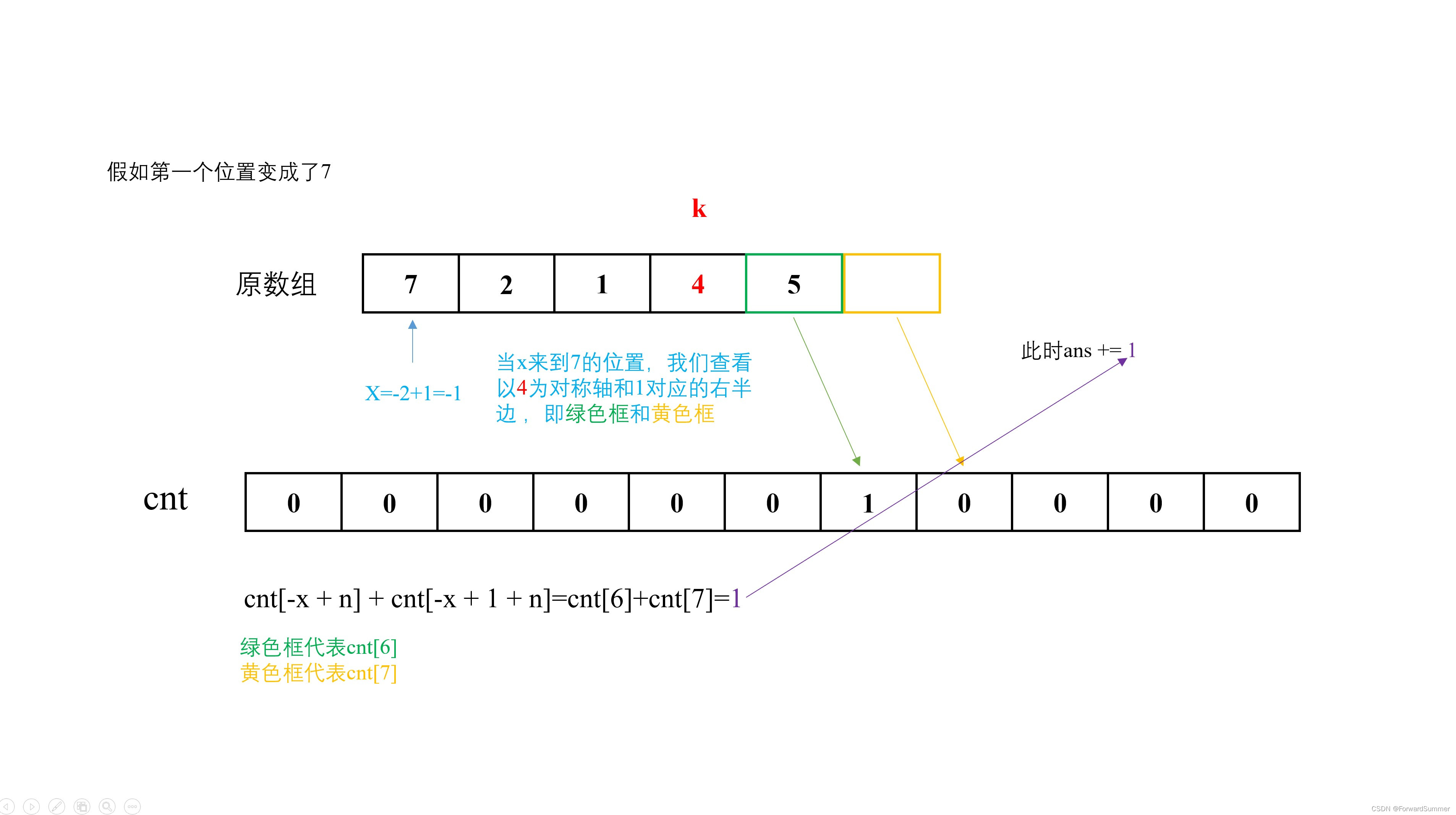
（8）###

参考来源

【1】leetcode 宫水三叶 前缀和 + 二分 运用题

【2】leetcode ylb [Python3/Java/C++/Go/TypeScript] 一题一解：遍历 + 计数（详细题解）

【3】leetcode 官方 长度最小的子数组 


http://www.kler.cn/a/1888.html

相关文章：

  • Python选择题训练工具：高效学习、答题回顾与音频朗读一站式体验
  • 深入解析：Python中的决策树与随机森林
  • nlp新词发现——浅析 TF·IDF
  • MongoDB 常用操作指南（Docker 环境下）
  • 论文《Vertical Federated Learning: Concepts, Advances, and Challenges》阅读
  • 【编辑器扩展】打开持久化路径/缓存路径/DataPath/StreamingAssetsPath文件夹
  • SAP 发出商品业务配置
  • 蓝桥杯备赛 [day01]｜python｜迷宫问题｜乘积尾零｜平方和｜切面条｜付账问题
  • 数据可视化
  • 数据库：mysql的主从复制实战
  • 版本管理工具git 与 svn 的区别具体有哪些？
  • UE实现地面动态交互效果
  • 大数据框架保姆级安装教程——Kafka（3.0.0）
  • 小白学Pytorch系列--Torch API (7)
  • Java单例模式写法
  • 差分运放公式推导-运算放大器
  • 初阶C语言：冒泡排序
  • typescript(元组、枚举、类、泛型)
  • mysql数据库常问面试题
  • 我的 System Verilog 学习记录（10）
  • CF1770E Koxia and Tree
  • 探索css渐变-实现饼图-加载图-灯柱
  • 【Java】UDP网络编程
  • 蓝桥杯算法全集之完全背包问题（动态规划算法）
  • 蓝桥杯真题——自动售水机
  • LeetCode：704. 二分查找