【数据结构】二叉树OJ题(C语言实现)

✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
🌟🌟 追风赶月莫停留 🌟🌟
🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀🍀
🌟🌟 平芜尽处是春山🌟🌟
🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟🌟
🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿🌿
✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨
✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅✅
📝数据结构OJ题
- ✏️单值二叉树
- ✏️相同的树
- ✏️二叉树前序遍历
- ✏️二叉树中序遍历
- ✏️二叉树后序遍历
✏️单值二叉树


class Solution {
public:
bool isUnivalTree(TreeNode* root)
{
if (root == NULL)
return true ;
if (root->left != NULL && root->val != root->left->val)
return false ;
if (root->right != NULL && root->val != root->right->val)
return false ;
return isUnivalTree(root->left)
&& isUnivalTree(root->right) ;
}
};
本题写法中,我们主要利用递归的思想和等号的性质从反向入手,也就是说只要有不相等就返回false。
上面说的等号的性质就是a=b,b=c那么a就一定等于c了。
如果从正向入手就有点麻烦,你判断了他们相等还要一个个的递归。大家可以去试一试。
当然还有一个最终要的条件判断,比较是在左子树和右子树都存在的情况下,如果不存在就不用比较,所以我在比较前都加了一个判断,判断root->left和root->right都存在,才去比较。
✏️相同的树

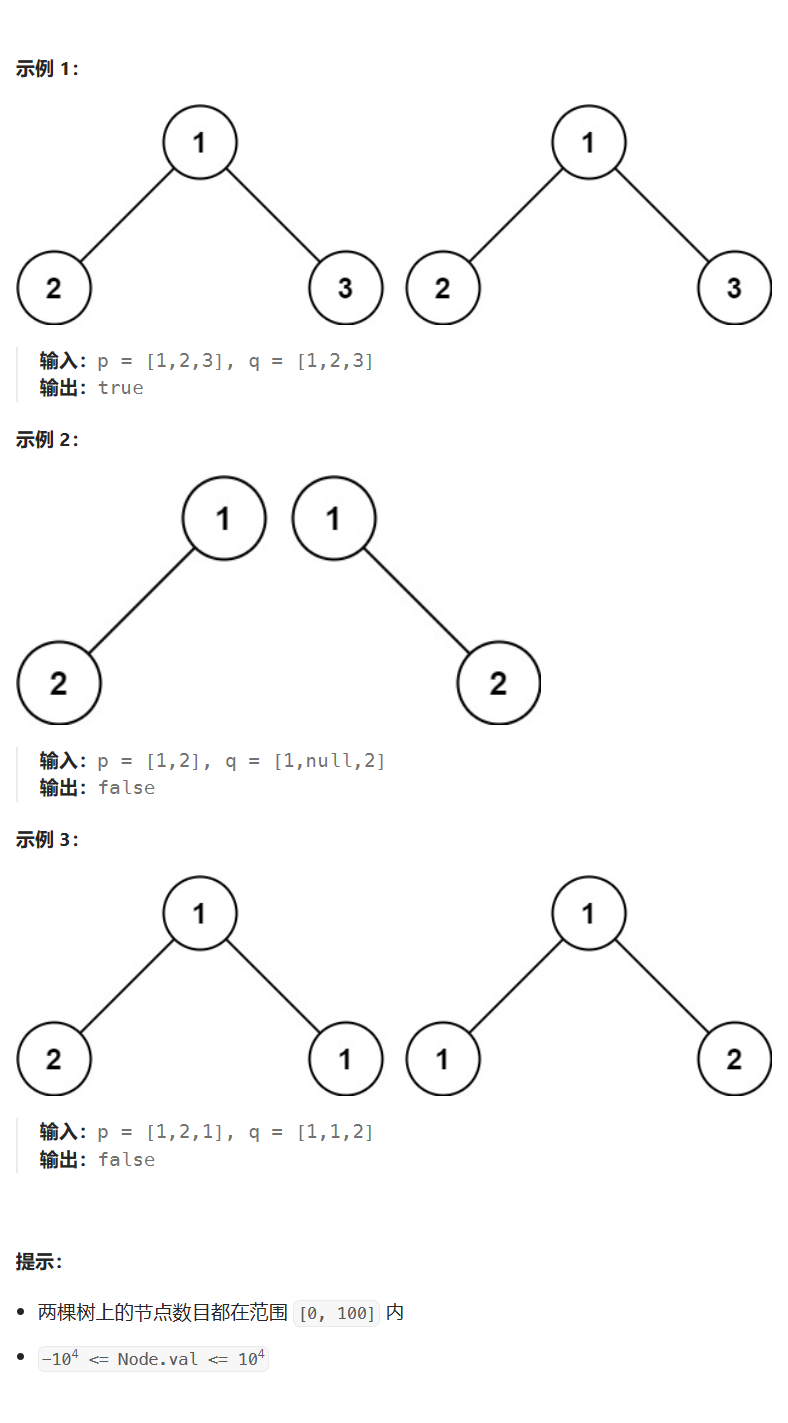
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q)
{
//两个都为空
if (p == NULL && q == NULL)
return true ;
//其中一个为空
if (p == NULL || q == NULL)
return false ;
if (p->val != q->val)
return false ;
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right) ;
}
};
上图是正确写法,还有一种常见的错误写法,下图是错误写法:
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q)
{
if (p == NULL && q == NULL)
return true ;
else
{
return false ;
}
if (p->val != q->val)
return false ;
return isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right) ;
}
};
两者最大的一个区别就是第一个判断哪里:
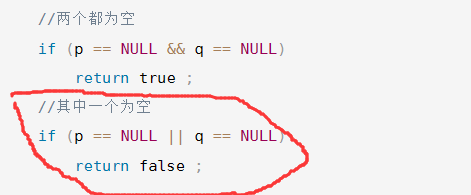

正确的写法是单独写了一个if来判断其中有一个为空,也就是有两种情况。要么是p为空,q不为空。要么就是p不为空,q为空。
错误的写法就是直接用了else,而这else包含了三种情况,比正确写法多包含了一种写法,就是两者都不为空的情况。
原本两者都不为空,才来比较,而错误写法中直接返回false了。
✏️二叉树前序遍历

//计算节点个数
int TreeSize(struct TreeNode *root)
{
if (root == NULL)
return 0 ;
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//进行前序遍历
void preorder(struct TreeNode *root, int *a, int *i)
{
if (root == NULL)
return ;
a[(*i)++] = root->val ;
preorder(root->left, a, i) ;
preorder(root->right, a, i) ;
}
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
int n = TreeSize(root) ;
int *a = (int *)malloc(sizeof(int)*n) ;
int j = 0 ;
preorder(root, a, &j) ;
*returnSize = n ;
return a ;
}
首先题目给出的:

这个可以简单理解为这个前序遍历所需要空间的大小,并不是系统提供的数组,系统内部有提供的有遍历所存放的数组,传过来的不是数组的地址,因为这是一级指针,改变不了系统所给数组里的数据,大家以后再遇到类似这个的时候都可以这样理解,所以我们开头就求了遍历所需要的空间大小:


以及在结尾,我又传给了returnSize。
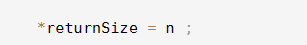
关于为什么这里传地址:

这是因为,这里的j是记录数组里面存放数据个数的,而我们这里前序遍历是利用递归实现的,而形参改变不了实参的大小,所以这里我传地址过去。
在这里进行前序遍历,我重新写了一个函数来实现:

前序遍历就是先执行根,然后左子树,最后右子树。
✏️二叉树中序遍历
//计算节点个数
int TreeSize(struct TreeNode *root)
{
if (root == NULL)
return 0 ;
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//进行中序遍历
void inorder(struct TreeNode *root, int *a, int *i)
{
if (root == NULL)
return ;
inorder(root->left, a, i) ;
a[(*i)++] = root->val ;
inorder(root->right, a, i) ;
}
int* inorderTraversal(struct TreeNode* root, int* returnSize)
{
int n = TreeSize(root) ;
int *a = (int *)malloc(sizeof(int)*n) ;
int j = 0 ;
inorder(root, a, &j) ;
*returnSize = n ;
return a ;
}
这里的中序遍历几乎和前序遍历一样,只是在递归的时候先递归左子树,然后赋值,最后递归右子树:


大家可以比较一下。
✏️二叉树后序遍历
//计算节点个数
int TreeSize(struct TreeNode *root)
{
if (root == NULL)
return 0 ;
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//进行后序遍历
void postorder(struct TreeNode *root, int *a, int *i)
{
if (root == NULL)
return ;
postorder(root->left, a, i) ;
postorder(root->right, a, i) ;
a[(*i)++] = root->val ;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize)
{
int n = TreeSize(root) ;
int *a = (int *)malloc(sizeof(int)*n) ;
int j = 0 ;
postorder(root, a, &j) ;
*returnSize = n ;
return a ;
}
大家可以仔细比较下,前中后序遍历的情况。
如果有错误,欢迎大家指针哈,我们一起学习进步!!!!!!

