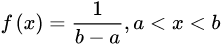当前位置：首页 > article >正文

数组、向量与矩阵

article 2024/11/15 12:28:49

问题缘起

在看《矩阵力量》的时候，写到

利用 a = numpy.array([4,3]). 严格说，此代码产生的不是行向量，运行 a.ndim 发现 a 只有一个维度。因此，转置 numpy.array([4,3]).T 得到的仍然是一维数组，只不过默认展示方式为行向量。

import numpy as np
a = np.array([4,3])
print(a)
 # [4 3]

那数组与向量有什么区别和联系？

理解数组

图示

1
数组 (Array)

定义：数组是一种线性表数据结构，它用一组连续的内存空间来存储一组具有相同类型的数据。
```
# 如果不是同一类型，NumPy 会自动改为同一类型
b1 = np.array(['3',4])
print(b1)
# ['3' '4']

b1 = np.array(['3',4,'str'])
print(b1)
# ['3' '4' 'str']

b1 = np.array(['3',4,'str',3.2])
print(b1)
# ['3' '4' 'str' '3.2']
```
数组：
- 定义：NumPy 是 Python 进行数值计算的核心库， ndarray （N维数组）是 NumPy 中最主要和最常用的数据结构。数组是一种线性表数据结构，它用一组连续的内存空间来存储一组具有相同类型的数据。除了存储在数组中的数据之外，该数据结构还包含有关数组的重要元数据，例如其形状、大小、数据类型以及其他属性。
  
  （ ps：NumPy还提供了其他一些数据结构，有 matrix、record 和 structured array、masked array、datetime64 和 timedelta64、char 和 string_、void）
- 维度：数组可以是多维的，包括一维数组、二维数组以及更高维的数组。最低是一维。

标量、向量、矩阵与张量

标量 Scalars

定义：在数学中，标量（英语：scalar）是指用来定义向量空间的域的一个元素。物理学中，标量（英语：scalar）又称纯量、无向量，是只有大小、没有方向、可用实数表示的一个量；按字面的意思，标量是以标尺度量出的量。在数学中，又称为数量。实际上标量就是数，这个称法只是为了区别于向量。标量可以是负数，例如温度低于冰点。与之相对，向量（又称矢量）既有大小，又有方向12。

例子：质量、电荷、体积、时间、速率、温度和某一点的电势。标量只有大小概念，没有方向的概念。通过一个具体的数值就能表达完整。

内置标量类型：如下所示。类似 C 的名称与字符代码相关联，这些代码显示在其描述中。然而，不鼓励使用字符代码。一些标量类型本质上等同于基本 Python 类型，因此继承自它们以及泛型数组标量类型13：

Array scalar type 数组标量类型	Related Python type 与python相关的类型	Inherits? 是否继承
`int_`	`int`	Python 2 only
`double`	`float`	yes
`cdouble`	`complex`	yes
`bytes_`	`bytes`	yes
`str_`	`str`	yes
`bool_`	`bool`	no
`datetime64`	`datetime.datetime`	no
`timedelta64`	`datetime.timedelta`	no

向量 vector

引用《编程不难》中的 13 章和《矩阵力量》第 2 章的内容，理解数组、向量和矩阵。

我们可以利用 numpy.array() 手动生成一维、二维、三维等数组。在 NumPy 中，array 是一种多维数组对象，它可以用于表示和操作向量、矩阵和张量等数据结构。

array 是 NumPy 中最重要的数据结构之一，它支持高效的数值计算和广播操作，可以用于处理大规模数据集和科学计算。与 Python 中的列表不同， array 是一个固定类型、固定大小的数据结构，它可以支持多维数组操作和高性能数值计算。

array 的每个元素都是相同类型的，通常是浮点数、整数或布尔值等基本数据类型。在创建 array 时，用户需要指定数组的维度和类型。例如，可以使用 numpy.array() 函数创建一个一维数组或二维数组，也可以使用 numpy.zeros() 函数或 numpy.ones() 函数创建指定大小的全 0 或全 1 数组，还可以使用 numpy.random 模块生成随机数组等。

除了基本操作之外，NumPy 还提供了许多高级的数组操作，例如数组切片、数组索引、数组重塑、数组转置、数组拼接和分裂等。

平面上，向量是有方向的线段。线段的长度代表向量的大小，箭头代表向量的方向。向量要么一行多列、要么一列多行，因此向量可以看做是特殊的矩阵——一维矩阵 (one-dimensional matrix)。一行多列的向量是行向量 (row vector)，一列多行的向量叫列向量 (column vector)。

一个矩阵可以视作由若干行向量或列向量整齐排列而成。数据矩阵 X 的每一行是一个行向量，代表一个样本点；X 的每一列为一个列向量，代表某个特征上的所有样本数据。

向量

定义：在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小和方向的量。在编程角度，向量只是具有单列或是单行的数组。
矩阵 matrix

定义：矩阵是由标量组成的矩形数组 (array)，也就是由由若干行或若干列元素组成。矩阵内的元素可以是实数、虚数、符号，甚至是代数式。从数据角度来看，矩阵就是表格！或者说，矩阵 X 可以看做是由一系列行向量 (row vector) 上下叠加而成。矩阵 X 也可以视作一系列列向量 (column vector) 左右排列而成。

行向量、列向量都是特殊矩阵。因此，行向量、列向量都是二维数组。
张量 tensor
定义：张量是一个多维数据容器，可以用来表示各种数据类型，如数值、图像、音频、文本等。

维度：张量的维度可以是任意的，包括零维（标量）、一维（向量）、二维（矩阵）以及更高维。

例子：一个三维张量（也称为三阶张量）可以看作是一个“立方体”的数据结构，每个元素由三个索引（如i、j、k）确定。在图像处理中，一张彩色图片可以表示为一个三维张量，其中两个维度表示图片的宽和高，第三个维度表示颜色通道（如RGB）14。

几何代数中定义的张量是基于向量和矩阵的推广，比如我们可以将标量视为零阶张量，矢量可以视为一阶张量，矩阵就是二阶张量15。

张量维度代表含义
0维张量代表的是标量（数字）
1维张量代表的是向量
2维张量代表的是矩阵
3维张量时间序列数据股价文本数据单张彩色图片(RGB)
张量是现代机器学习的基础。它的核心是一个数据容器，多数情况下，它包含数字，有时候它也包含字符串，但这种情况比较少。因此可以把它想象成一个数字的水桶。这里有一些存储在各种类型张量的公用数据集类型：
- 3维 = 时间序列
- 4维 = 图像
- 5维 = 视频
在有些语境下，更高维度的数组叫张量 (tensor)，因此向量和矩阵可以分别看作是一维和二维的张量。张量是多维数组，目的是把向量、矩阵推向更高的维度。
区别与联系
- 数组是张量。
  
  任何数组都可以被视为一个张量，但并非所有张量都可以简单地被视为数组。因为张量可以具有任意数量的维度（从0维到任意高维），而数组通常只被限制为一维到多维。并且数组只包含相同类型的数据，而张量包含不同类型的数据。
- 向量的维度和数组矩阵张量的维度代表的意思是不同的。
  1. 向量的维度代表空间复杂度，是坐标的数量。
  2. 数组的维数指数组中不同维度的个数。一维数组在单一方向上延伸（例如一个线性列表），二维数组同时拥有两个维度（即多行多列）。
  3. 矩阵的维数是指它的行数与列数。例如，一个2x3的矩阵有2行和3列，因此其维数是2x3。
  4. 张量的维度数是指其具有的坐标轴的数量。
    - 一维张量（向量）：只有一个坐标轴，可以看作是一维数组。例如，[1, 4, 3, 2, 5] 是一个一维张量（向量），其维度为1。
    - 二维张量（矩阵）：有两个坐标轴，可以看作是二维数组或表格。例如，[[1, 2, 3], [4, 5, 6], [7, 8, 9]] 是一个二维张量（矩阵），其维度为2。
    - 一个三维张量可以看作是一个“矩阵的矩阵”，或者是一个包含多个二维数组的数组。在形状上，三维张量通常表示为(深度, 高度, 宽度)，其中每个维度都对应一个坐标轴。
- numpy的ndarray类用于表示矩阵和向量。a=np.random.randn(5)，这样会生成存储在数组 a 中的5个高斯随机数变量。之后输出 a，从屏幕上可以得知，此时 a 的shape（形状）是一个(5,)的结构。这在Python中被称作一个一维数组。它既不是一个行向量也不是一个列向量16，但是在形式上很像，简单图示如下17。
```
a=np.random.randn(5)
print(a)  # [ 0.17712589  1.19730274  0.85170878 -0.98597119  0.42512271]
print(a.shape) # (5,)
print(a.T)        # [ 0.17712589  1.19730274  0.85170878 -0.98597119  0.42512271]
print(a.T.shape)  # (5,)
print(np.dot(a,a.T))    # 3.343183794342581

# b 是行向量，a 是一维数组
b = a.reshape(1,-1)
print(b.shape) # (1, 5)

#产生随机的一维数组
c1 = np.random.rand(5)  
print(c1)
# [0.46640684 0.84288213 0.26926843 0.14286057 0.51266955]

#产生的4行1列的列向量
c2 = np.random.randn(4,1) 
print(c2)
"""
[[-1.12026069]
 [-0.3329943 ]
 [-0.98272641]
 [-1.9171402 ]]
"""

# 产生的1行4列的行向量
c3 = np.random.randn(1,4) #产生的1行5列的行向量
print(c3)
# [[-0.3876463  -0.43556247  0.76948215 -0.96267679]]
```
- Numpy中的数组shape为（m,）说明它是一个一维数组，或者说是一个向量，不区分列向量还是行向量，在与矩阵进行矩阵乘法时，numpy会自动判断此时的一维数组应该取行向量还是列向量17。
```
X = np.random.randn(4,3) # X.shape:(4, 3)
t = np.array([2,3,4])
 # t.shape:(3,),此时不区分行向量还是列向量

  y = X.dot(t) 
# 计算矩阵与向量乘法时，会把t当做列向量来计算,此时结果仍然是一维数组（但我们知道，这个结果应该是列向量）
```
  在numpy中，用二维矩阵而不是一维矩阵来表示行向量和列向量：
  
  行向量的形状：(n, 1)
  
  列向量的形状：(1, n)
```
X = np.random.randn(4,3) # X.shape:(4, 3)
t = np.array([2,3,4]).reshape(3,1) # t.shape:(3,1),表示是列向量
y = X.dot(t) # y.shape:(4,1),表示结果也是列向量
```
  计算线性方程组：
```
# y = 4 + 2*x1 + 3*x2 + x3
X = np.random.randn(4,3)
X_b = np.c_[np.ones((4,1)), X] #构造矩阵，增加x0=1
t = np.array([4,2,3,1]).reshape(4,1)
y = X_b.dot(t)
```

张量维度	代表含义
0维张量	代表的是标量（数字）
1维张量	代表的是向量
2维张量	代表的是矩阵
3维张量	时间序列数据股价文本数据单张彩色图片(RGB)

数组

理解数组的生成函数、数据类型、索引、维度与轴。

生成随机数组

创建一个数组的最简单方式是使用array函数。它接受任何序列对象（包括其它数组），产生一个新的包含传入数据的NumPy数组2。

In [1]: data1 = [6, 7.5, 8, 0, 1]
In [2]: arr1 = np.array(data1)
In [3]: arr1
Out[3]: array([ 6. , 7.5, 8. , 0. , 1. ])

嵌套序列，如等长度列表的列表。将转换成一个多维数组:

In [22]: data2 = [[1, 2, 3, 4], [5, 6, 7, 8]]
In [23]: arr2 = np.array(data2)
In [24]: arr2
Out[24]:array([[1, 2, 3, 4]
               ,[5, 6, 7, 8]])

由于data2是一个列表的列表，因此从数据推断 NumPy 数组 arr2 有有两个维度的 shape。我们可以通过检查 ndim 和 shape 属性来验证这个:

In [25]: arr2.ndim
Out[25]: 2

In [26]: arr2.shape
Out[26]: (2, 4)

除非明确指定，否则 np.array 尝试为它创建的数组推断一个合适的数据类型。数据类型是被储存在特殊的元数据对象 dtype 中；举例，在之前的两个例子中我们有:

In [27]: arr1.dtype
Out[27]: dtype('float64')

In [28]: arr2.dtype
Out[28]: dtype('int64')

除了 np.array 还有许多其它函数可以创建新数组。例如 zeros 和 ones 分别创建全 0 或全 1 的数组，使用给定的长度或 shape。empty 创建没有初始化值到具体值的数组。为了用这些方法创建更高维度的数组，传一个元组给 shape:

In [29]: np.zeros(10)
Out[29]: array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.])

In [30]: np.zeros((3, 6))
Out[30]:
array([[ 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0.]])

In [31]: np.empty((2, 3, 2))
Out[31]:
array([[[ 0., 0.],
[ 0., 0.],
[ 0., 0.]],
[[ 0., 0.],
[ 0., 0.],
[ 0., 0.]]])

arange 是 Python 内建 range 函数的一个数组值版本:

In [32]: np.arange(15)
Out[32]: array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])

创建数组的函数

函数说明	默认直接复制输入数据.
array	将输入数据（列表、元组、数组或其它序列类型）转换为 ndarray。要么推断出 dtype，要么特别指定 dtype。
asarray	将输入转换为 ndarray，如果输入本身就是一个 ndarray 就不进行复制
arange	类似于内置的 range，但返回的是一个 ndarray 而不是列表
ones, ones_like	根据指定的形状和 dtype 创建一个全1数组。one_like 以另一个数组为参数，并根据其形状和 dtype 创建一个全数组。
zeros, zeros_like	类似于 ones 和 ones _like，只不过产生的是全0数组而已
empty, empty_like	创建新数组，只分配内存空间但不填充任何值
full, full_like	用 fill value 中的所有值，根据指定的形状和 dtype 创建一个数组。full_like 使用另一个数组，用相同的形状和 dtype 创建
eye ,identity	创建一个正方的 N*N 单位矩阵（对角线为1，其余为0）

另外的总结，参考https://vlight.me/2018/03/20/Numerical-Python-vectors-matrices-and-arrays/。

函数名	数组类型
np.array	创建一个数组，其中元素由一个类数组（array-like）对象给出，例如，它可以是 Python 列表、元组、可迭代序列或另一个 ndarray 实例。
np.zeros	创建一个指定维度和数据类型的数组，并将其填充为0
np.ones	创建一个指定维度和数据类型的数组，并将其填充为1
np.diag	创建一个对角阵，指定对角线上的值，并将其他地方填充为0
np.arange	指定开始值、结束值和增量，创建一个具有均匀间隔数值的数组
np.linspace	使用指定数量的元素，在指定的开始值和结束值之间创建一个具有均匀间隔数值的数组
np.logspace	指定开始值和结束值，创建一个具有均匀对数间隔值的数组
np.meshgrid	使用一维坐标向量生成坐标矩阵（和更高维坐标数组）
np.fromfunction	创建一个数组，并用给定函数的函数值填充
np.fromfile	创建一个数组，其数据来自二进制（或文本）文件，NumPy 还提供相应的将 NumPy 数组存储在硬盘中的函数 `np.tofile`
np.genfromtxt, np.loadtxt	创建一个数组，其数据读取子文本文件，如 CSV 文件，`np.genfromtxt` 也支持处理缺失值
np.random.rand	创建一个数组，其值在 (0, 1) 之间均匀分布

数组的数据类型

ndarray数据类型

数据类型或dtype是一类特殊的对象，包含信息（或元数据，关于数据的数据）ndarray需要将一块内存解释为特定的数据类型:

In [33]: arr1 = np.array([1, 2, 3], dtype=np.float64)
In [34]: arr2 = np.array([1, 2, 3], dtype=np.int32)
In [35]: arr1.dtype
Out[35]: dtype('float64')
In [36]: arr2.dtype
Out[36]: dtype('int32')

dtype 是 NumPy 与其它系统交互数据的灵活性来源。在大多数情况下，它们直接映射到底层磁盘或内存表示，可以轻松读取和写入二进制数据流数据到磁盘以及连接到用C或Fortran等低级语言编写的代码。 dtype 数值以相同方式命名：一个类型名如 float 或 int，随后是一个表明每个元素占多少位的数字。标准双精度浮点数占8个字节或64位。因此，这种类型在 NumPy 中被命名为 float64。见下表 NumPy 支持的数据类型全面清单。

注：不要担心记忆 NumPy 数据类型，尤其是你现在还是一个新手时。仅仅有必要关心你正在处理的通用数据种类，是浮点数。复数、整型、布尔型还是一般的 Python 对象。当你需要更多地控制在磁盘和内存中数据储存方式时，特别是大型数据集，最好知道你控制的储存类型。

类型	类型代码	说明
int8, uint8	i1,u1	有符号和无符号的8位（1个字节）整型
int16, uint16	i2, u2	有符号和无符号的16位（2个字节）整型
int32. uint32	i4, u4	有符号和无符号的32位（4个字节）整型
int64. uint64	i8, u8	有符号和无符号的64位（8个字节）整型
float 16	f2	半精度浮点数
float32	f4或f	标准的单精度浮点数。与C的float兼容
float64	f8或d	标准的双精度浮点数。与C的double和Python 的float对象兼容
float128	f16或g	扩展精度浮点数
complex64, complex128, complex256	c8, c16,c32	分别用两个32位、64位或128位浮点数表示的复数
bool	?	存储True和False值的布尔类型
object	O	Python对象类型
string_	S	固定长度的字符串类型（每个字符1个字节）。例如，要创建一个长度为10的字符串，应使用 S10
unicode_	U	固定长度的unicode类型（字节数由平台决定）。跟字符串的定义方式一样（如U10）

显式转换或铸造 (cast) 一个数组从一种dtype到另一种，使用 ndarray 的 adtype 方法:

In [37]: arr = np.array([1, 2, 3, 4, 5])

In [38]: arr.dtype
Out[38]: dtype('int64')

In [39]: float_arr = arr.astype(np.float64)

In [40]: float_arr.dtype
Out[40]: dtype('float64')

在这个例子中，整型被转换成浮点型。如果我转换一些浮点数字到一个整型 dtype，小数部分将被丢弃:

In [41]: arr = np.array([3.7, -1.2, -2.6, 0.5, 12.9, 10.1])

In [42]: arr
Out[42]: array([ 3.7, -1.2, -2.6, 0.5, 12.9, 10.1])

In [43]: arr.astype(np.int32)
Out[43]: array([ 3, -1, -2, 0, 12, 10], dtype=int32)

如果你有代表数字的字符串数组，你可以使用astype转换它们到数值形式：

In [44]: numeric_strings = np.array(['1.25', '-9.6', '42'], dtype=np.string_)

In [45]: numeric_strings.astype(float)
Out[45]: array([ 1.25, -9.6 , 42. ])

数组的维度与轴

维度：在 NumPy 中，维度称为轴。Numpy库的核心是ndarray，实际上就是N维数组（N-dimensional array）。轴(Axis）是一个非常重要的概念，它贯穿于Numpy数组(ndarray）的各种操作中[3-5]。
轴的定义和作用。在Numpy中，轴通常指的是数组的维度。对于一个多维数组，我们可以沿着不同的维度(即轴）进行各种操作，如求和、平均值计算、最大值查找等。轴的作用是确定这些操作是沿着哪个方向进行的。
维度与轴。Numpy 数组可以是—维的、二维的，甚至是更高维度的。一维数组只有一个轴，二维数组有两个轴(通常称为行和列，第一个轴成为行轴，第二个轴成为列轴)，以此类推。每个轴都有一个与之关联的索引，从 0 开始，按照数组维度的顺序递增。

1. 图示

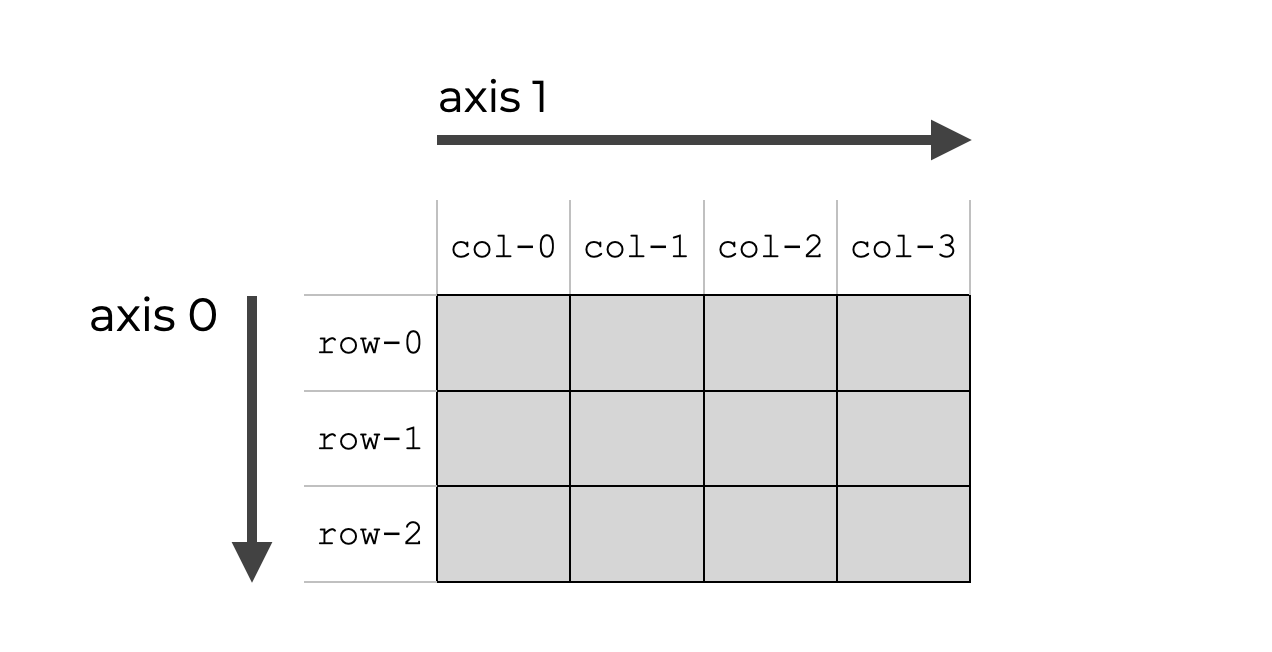
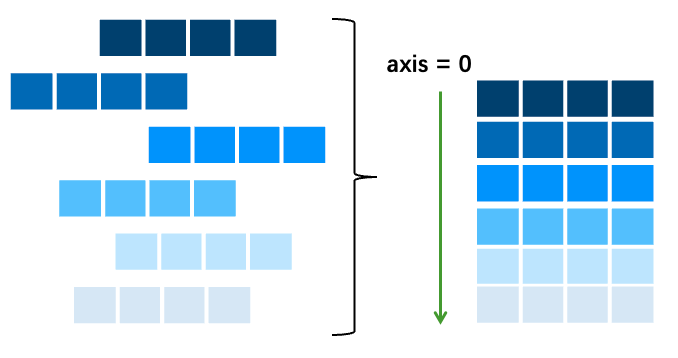
多维数组的轴。轴 0 是“第一轴”，轴 0 是沿着行向下延伸的轴，这适用于二维数组和多维数组，一维数组是一种特殊情况。

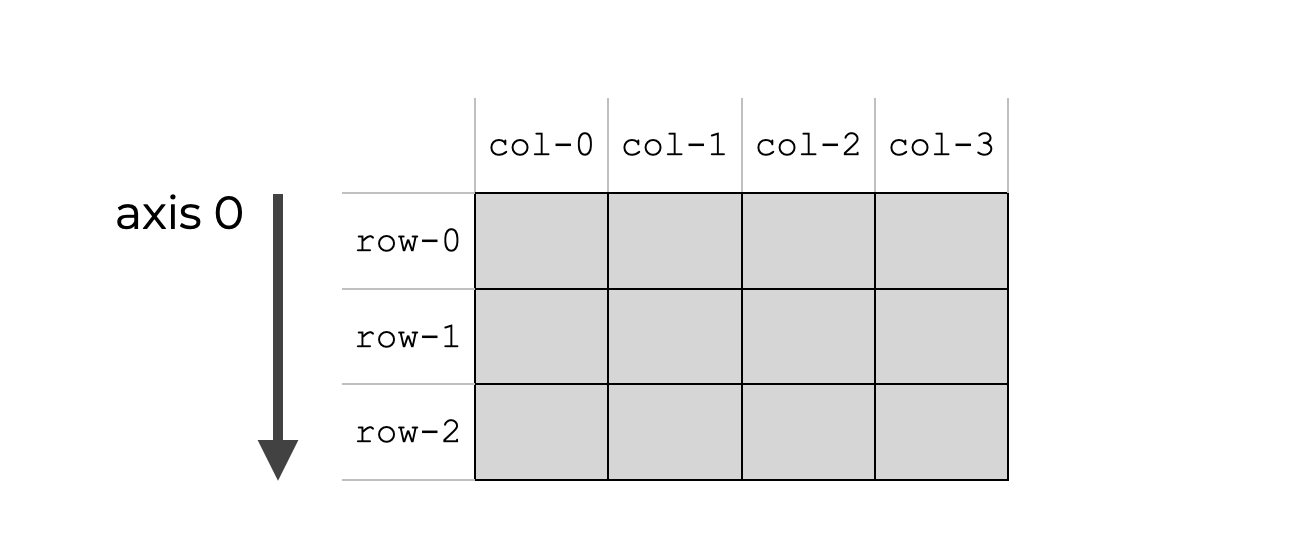
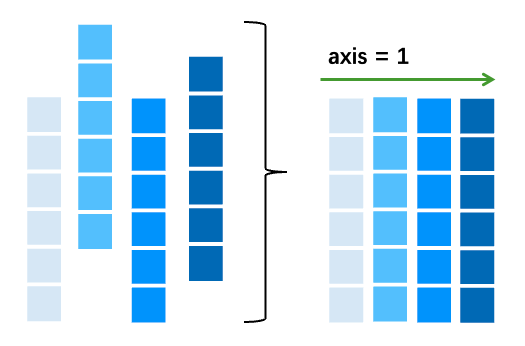
轴 1 是第二个轴，是水平穿过列的轴。

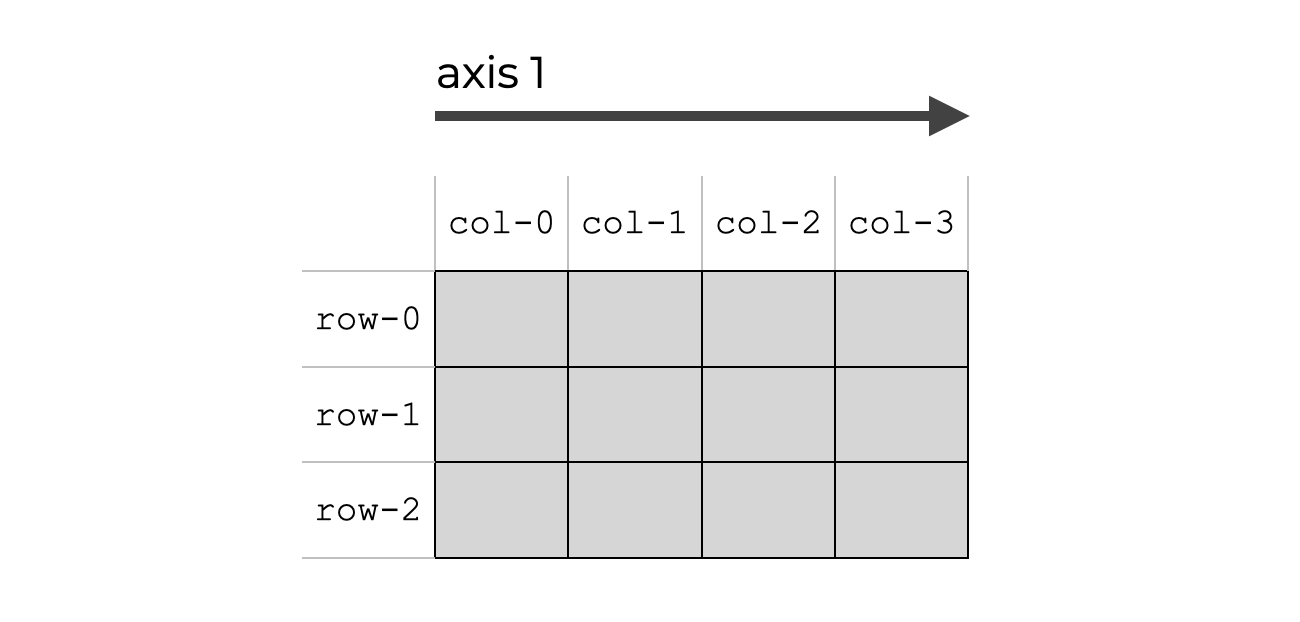
再次图解，参考矩阵力量。轴 0 是沿行向下延伸的方向。

轴 1 是沿列穿过的的方向。

2. 代码角度理解

从代码角度看一下 NumPy 轴在NumPy sum 函数内部如何工作。当尝试理解 NumPy sum 中的轴时，您需要知道axis参数实际控制什么。在np.sum()中， axis参数控制将聚合哪个轴。换句话说， axis参数控制哪个轴将被折叠。

请记住， sum() 、 mean() 、 min() 、 median()等函数以及其他统计函数会汇总您的数据。为了解释“聚合”的含义。举一个简单的例子，假设有一组 5 个数字。如果将这 5 个数字相加，结果将是一个数字。求和有效地聚合您的数据。它将大量值折叠为单个值。

类似地，当您在带有axis参数的二维数组上使用np.sum()时，它会将二维数组折叠为一维数组。它将折叠数据并减少维数。但哪个轴会塌陷呢？当您将 NumPy sum 函数与axis参数一起使用时，您指定的轴是折叠的轴。

当轴 = 0 的 Numpy 求和

  # 它是一个简单的二维数组，其中有 6 个值以 2 x 3 的形式排列。
  np_array_2d = np.arange(0, 6).reshape([2,3])
  print(np_array_2d)
  '''
  [[0 1 2]
   [3 4 5]]
  '''
  np.sum(np_array_2d, axis = 0)
  # array([3, 5, 7])
  print(np.sum(np_array_2d, axis = 0))
  # [3 5 7]

当我们设置axis = 0时，该函数实际上对列进行求和。结果是一个新的 NumPy 数组，其中包含每列的总和。为什么？轴 0 不是指行吗？

这让很多初学者感到困惑，所以让我解释一下。

正如之前提到的， axis参数指示哪个轴被折叠。因此，当我们设置axis = 0时，我们不会对各行进行求和。当我们设置axis = 0时，我们正在聚合数据，以便折叠行……我们折叠轴 0。

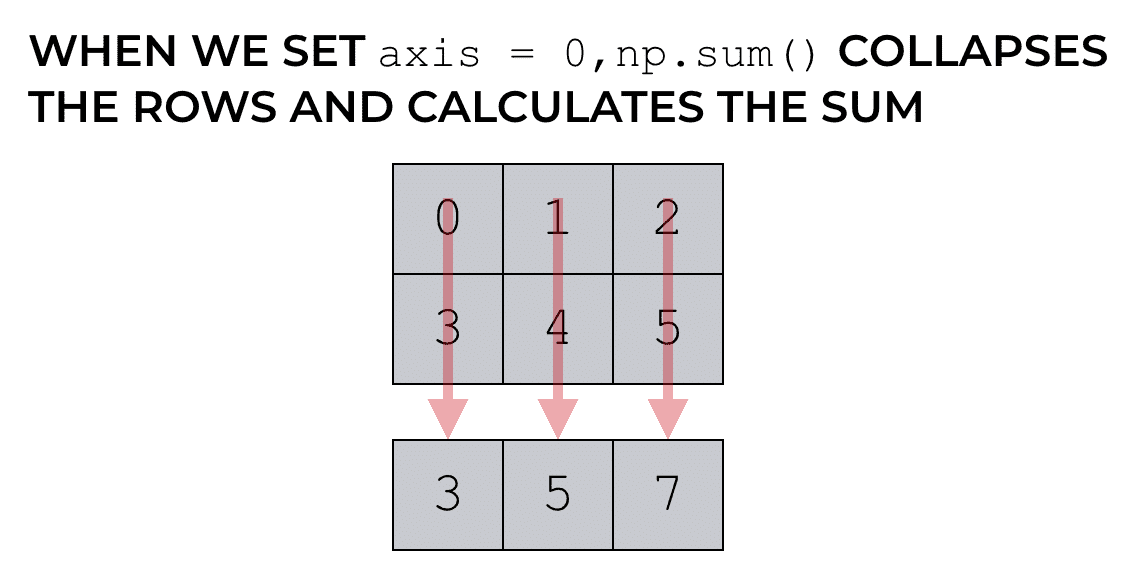
当轴 = 1 的 Numpy 求和

同样，使用sum()函数， axis参数设置在求和过程中折叠的轴。轴 1 指的是跨列的水平方向。这意味着代码np.sum(a, axis = 1)在求和期间折叠列。

  np.sum(np_array_2d, axis = 1)
  # array([3, 12])
 
  print(np.sum(np_array_2d, axis = 1)) 
  # [ 3 12] 
  
  # 也可以写
  np_array_2d.sum(axis = 1)
  # array([3, 12])

正如之前提到的，这让许多初学者感到困惑。他们期望通过设置axis = 1 ，NumPy 将对列进行求和，但这不是它的工作原理。该代码具有跨列求和的效果。它折叠轴 1。

imh8

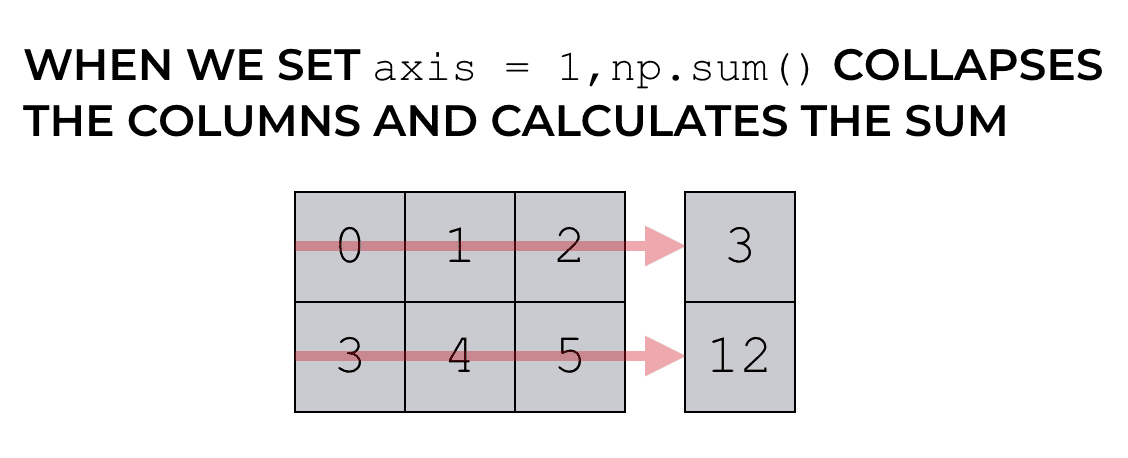
showmeai 也有类似图示。

3. 扩展（理解轴在连接数组的时候的作用）

使用 NumPy 连接函数，连接两个二维 NumPy 数组，使用 axis 参数。

  np_array_1s = np.array([[1,1,1],[1,1,1]])
  np_array_1s
  '''
   array([[1, 1, 1],
         [1, 1, 1]])
  '''
  
  np_array_9s = np.array([[9,9,9],[9,9,9]])
  np_array_9s
  '''
  array([[9, 9, 9],
         [9, 9, 9]])
  '''

NumPy 数组连接轴 axis = 0，使用 concatenate 函数时， axis参数定义我们堆叠数组的轴。因此，当我们设置axis = 0时，我们告诉连接函数将两个数组沿行堆叠。我们指定要沿轴 0 连接数组。

  np.concatenate([np_array_1s, np_array_9s], axis = 0)
  
  '''
  array([[1, 1, 1],
      [1, 1, 1],
         [9, 9, 9],
         [9, 9, 9]])
  '''

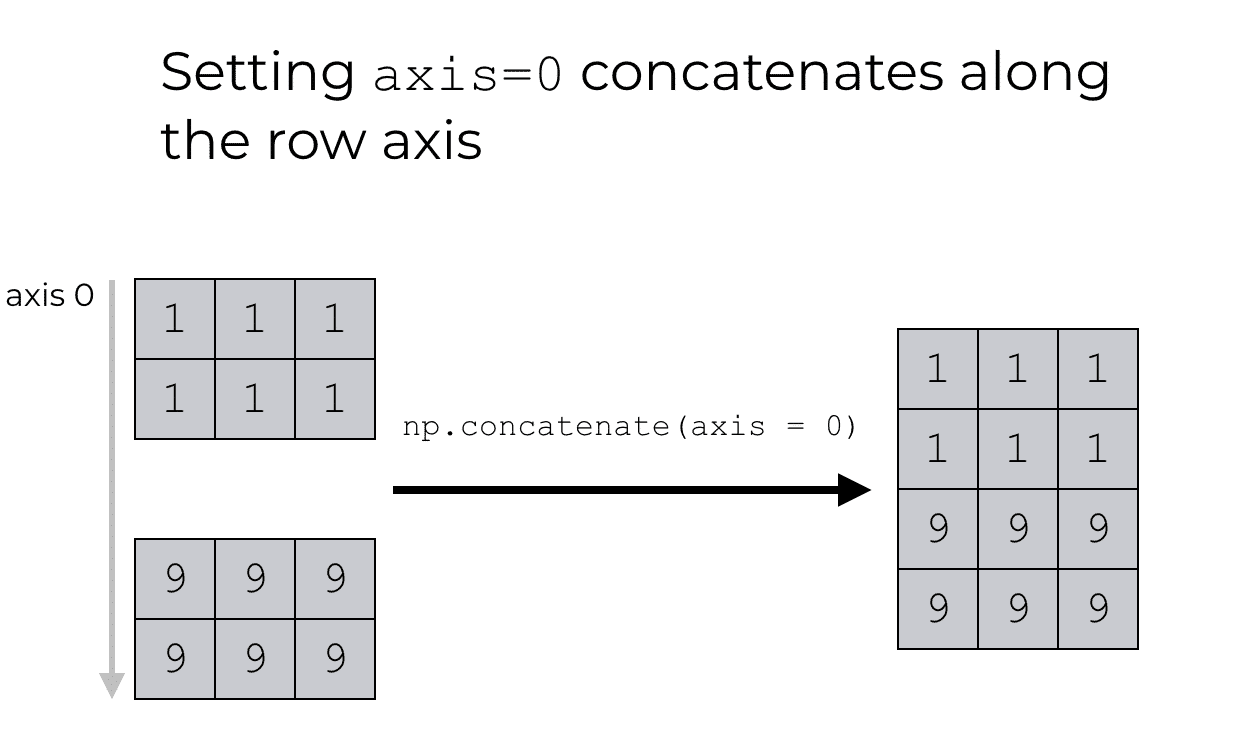
连接轴 axis = 1，使用 concatenate 函数时，轴 1 是水平穿过 NumPy 数组列的轴。

  np.concatenate([np_array_1s, np_array_9s], axis = 1)
  '''
  array([[1, 1, 1, 9, 9, 9],
      [1, 1, 1, 9, 9, 9]])
  '''

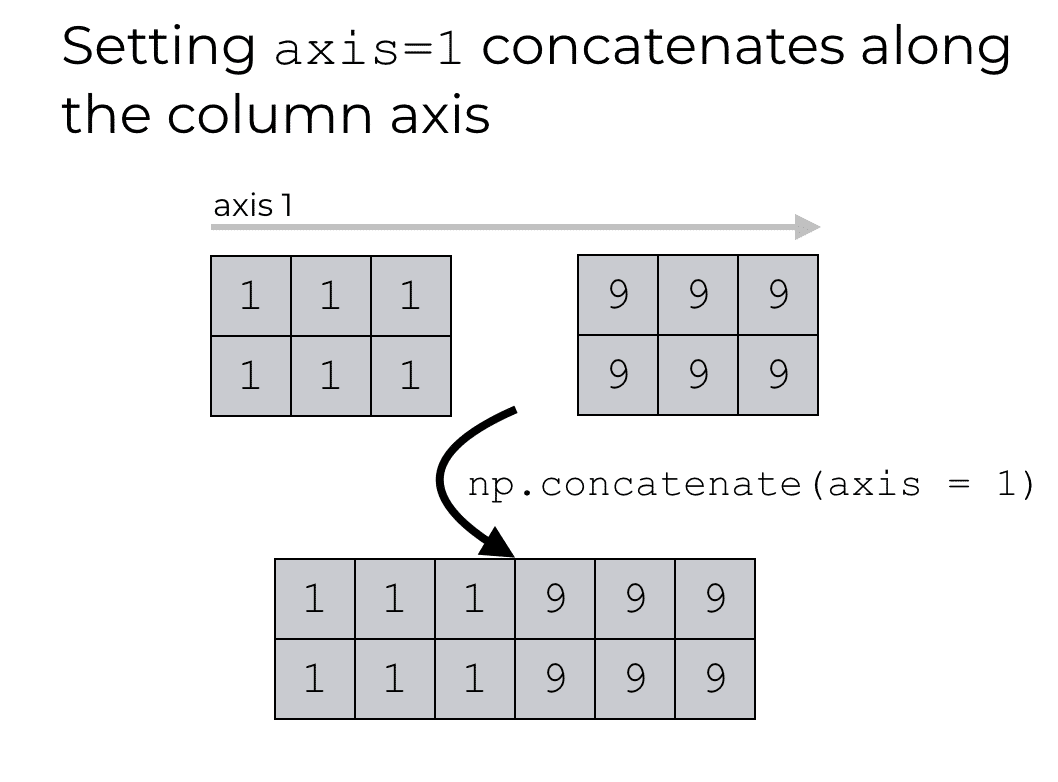
3. 扩展（理解一维数组）

一维 NumPy 数组只有一个轴。轴的编号方式与 Python 索引类似。他们从 0 开始。因此，在一维 NumPy 数组中，第一个也是唯一的轴是轴 0。

创建两个一维数组

  np_array_1s_1dim = np.array([1,1,1])
  np_array_9s_1dim = np.array([9,9,9])
 
  print(np_array_1s_1dim) #  [1 1 1]
  
  print(np_array_9s_1dim) # [9 9 9]

接下来，让我们使用np.concatenate()和axis = 0将它们连接在一起。

  np.concatenate([np_array_1s_1dim, np_array_9s_1dim], axis = 0)
  '''
  array([1, 1, 1, 9, 9, 9])
  '''

这个输出让许多初学者感到困惑。这些数组水平连接在一起。这与该函数在二维数组上的工作方式不同。如果我们在二维数组上使用axis = 0的np.concatenate() ，数组将垂直连接在一起。这是怎么回事？

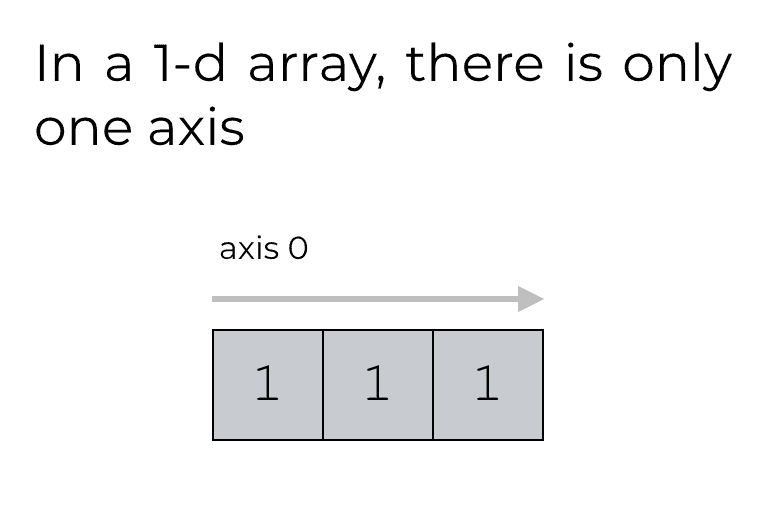
一维 NumPy 数组只有一个轴。轴 0。在这种情况下该功能可以正常工作。 NumPy concatenate是沿着轴 0 连接这些数组。问题是在一维数组中，轴 0 不像在二维数组中那样指向“向下”。

尝试一下：

  np.concatenate([np_array_1s_1dim, np_array_9s_1dim], axis = 1)
  #  此代码会导致错误：
  #  AxisError: axis 1 is out of bounds for array of dimension 1

np_array_1s_1dim和np_array_9s_1dim是一维数组。因此，它们没有轴 1 。我们尝试在这些数组中不存在的轴上使用np.concatenate() 。因此，该代码会产生错误。

所有这些都表明，在使用一维数组时需要小心。当您使用一维数组，并且使用一些带有axis参数的 NumPy 函数时，代码可能会生成令人困惑的结果。如果您真正了解 NumPy 轴的工作原理，那么结果会很有意义。但如果您不理解 NumPy 数组轴，结果可能会令人困惑。因此，在开始使用 NumPy 数组轴之前，请确保您真正理解它们！

数组切片和索引

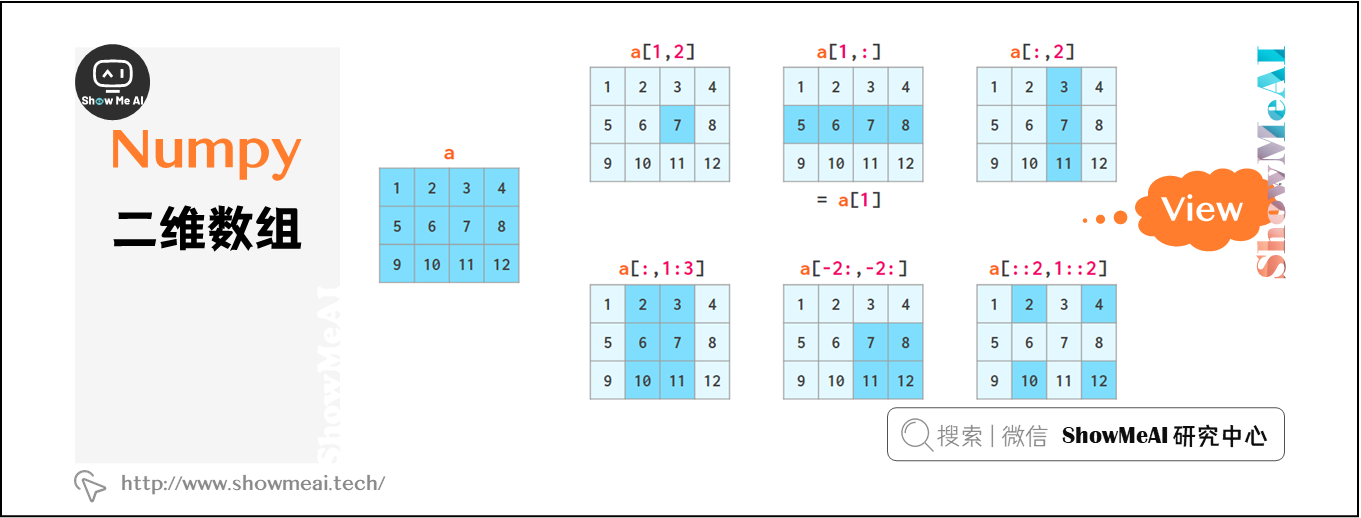
1. 图示

我们将元素在数组中的位置称为该元素的索引（index）。下图展示了数组的主要概念和存储方式。数组索引语法与列表类似，二维数组的索引语法要比嵌套列表更方便6。

a 是一个二维的数组

a = np.array([
    [1,2,3,4],[5,6,7,8],[9,10,11,12]
])
print(a)

'''
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
'''

a[1,2]
# 7

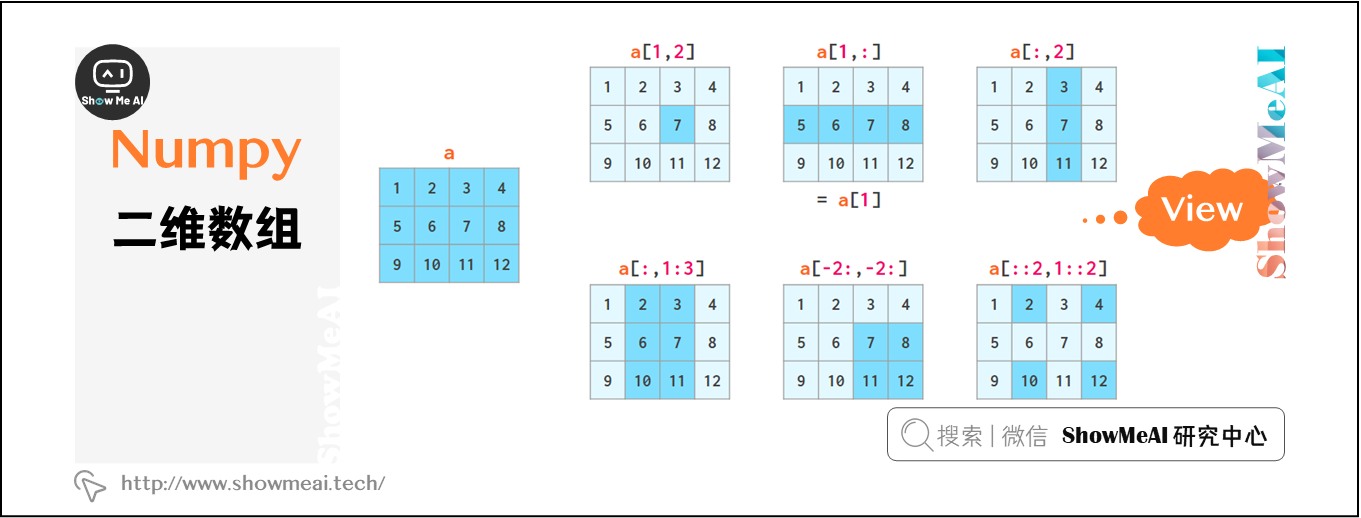
view 表示数组切片时并未进行任何复制，在修改数组后，相应更改也将反映在切片中。

2. 多维数组的切片和索引

1. 切片(slicing)操作

Numpy 中多维数组的切片操作与 Python 中 list 的切片操作一样，同样由 start, stop, step 三个部分组成7。

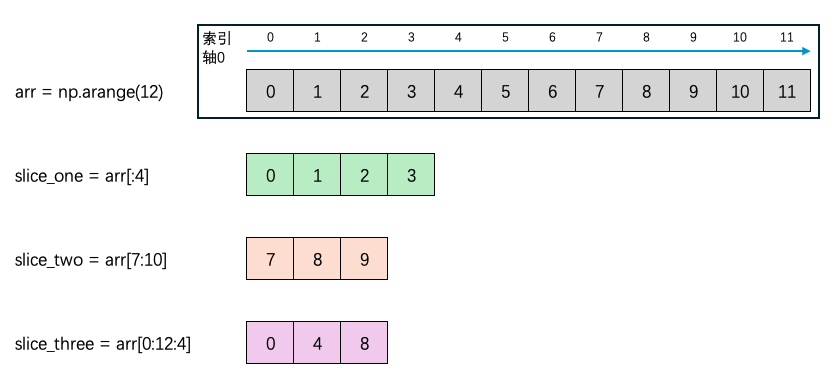
一维数组的例子：

import numpy as np
   
arr = np.arange(12)
print('array is:', arr)
   
slice_one = arr[:4]
print ('slice begins at 0 and ends at 4 is:', slice_one)
   
slice_two = arr[7:10]
 # [7:10] 是不包括10的
print ('slice begins at 7 and ends at 10 is:', slice_two)
   
slice_three = arr[0:12:4]
print ('slice begins at 0 and ends at 12 with step 4 is:', slice_three)
print(arr[::4])
 
'''
array is: [ 0  1  2  3  4  5  6  7  8  9 10 11]
slice begins at 0 and ends at 4 is: [0 1 2 3]
slice begins at 7 and ends at 10 is: [7 8 9]
slice begins at 0 and ends at 12 with step 4 is: [0 4 8]
   [0 4 8]
   '''

如果是多维数组，将不同维度上的切片操作用逗号分开就好了

arr = np.arange(12).reshape((3, 4))
print ('array is:',arr)

'''
array is: [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
'''


# 取第一维的索引 1 到索引 2 之间的元素，也就是第二行
# 取第二维的索引 1 到索引 3 之间的元素，也就是第二列和第三列
slice_one = arr[1:2, 1:3]
print ('first slice is:',slice_one)
# first slice is: [[5 6]]



# 取第一维的全部
# 按步长为 2 取第二维的索引 0 到末尾 之间的元素，也就是第一列和第三列
slice_two = arr[:, ::2]
print ('second slice is:',slice_two)
"""
second slice is: [[ 0  2]
 [ 4  6]
 [ 8 10]]
"""

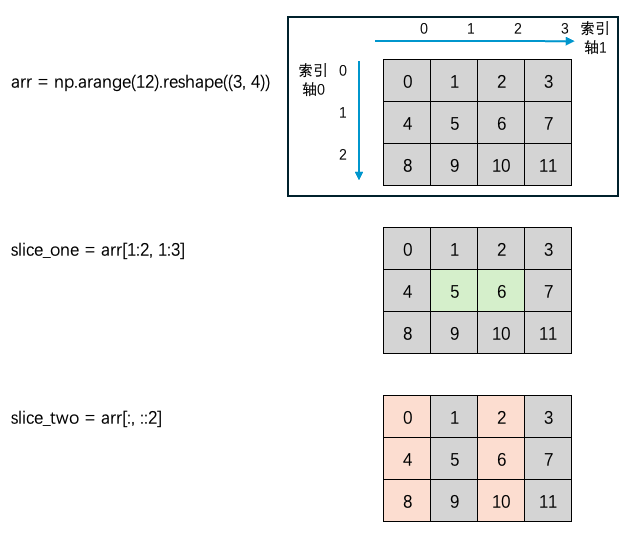
对于 slice_two，如果 arr 是用 Python 的 list 表示的，那么要得到相同的结果得像下面这样，相对来说就麻烦多了:

arr = np.arange(12).reshape((3, 4)).tolist()
print(arr)

# [[0, 1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11]]


slice_two = [
    row[::2] for row in arr
]
print(slice_two)
# [[0, 2], [4, 6], [8, 10]]

对于维数超过 3 的多维数组，还可以通过 ‘…’ 来简化操作

arr = np.arange(24).reshape((2, 3, 4))

print (arr[1, ...])              # 等价于 arr[1, :, :]
print("**************")
print (arr[..., 1])               # 等价于 arr[:, :, 1]

"""
[[12 13 14 15]
 [16 17 18 19]
 [20 21 22 23]]
**************
[[ 1  5  9]
 [13 17 21]]
"""

2. 索引(indexing) 操作

最简单的情况

对于一个多维数组来说，最简单的情况就是访问其中一个特定位置的元素了，如下所示:

arr = np.array([
    [1, 2, 3, 4],
    [2, 4, 6, 8],
    [3, 6, 9, 12],
    [4, 8, 12, 16]
])
print('第二行第二列的值:', arr[1, 1])
# 第二行第二列的值: 4

相比之下，如果用 Python 的 list 来表示上述二维数组，获取同一个位置的元素的方法为:

arr = [
    [1, 2, 3, 4],
    [2, 4, 6, 8],
    [3, 6, 9, 12],
    [4, 8, 12, 16]
]
print ('第二行第二列的值:', arr[1][1])
print('------------------')
try:
    print ('第二行第二列的值(尝试用 Numpy 的方式获取):', arr[1, 1])
except Exception as e:
    print (str(e))
    
"""
第二行第二列的值: 4
------------------
list indices must be integers or slices, not tuple
"""

element = arr_list[2][1]  # 获取第三行第二列的元素
print(element)  # 输出: 6

# 用嵌套列表表示二维数组。
# 通过 arr_list[row][column] 的方式获取同一个位置的元素。

如果只是二维数组，这种差别可能看起来并不大，但想象一下假如有一个 10 维的数组，用 Python 的标准做法需要写 10 对中括号，而用 Numpy 依然只需要一对。

获取多个元素

事实上，在 Numpy 的索引操作方式 x = arr[obj] 中， obj 不仅仅可以是一个用逗号分隔开的数字序列，还可以是更复杂的内容。

用逗号分隔的数组序列
- 序列的长度和多维数组的维数要一致
- 序列中每个数组的长度要一致
```
import numpy as np

arr = np.array([
    [1, 2, 3, 4],
    [2, 4, 6, 8],
    [3, 6, 9, 12],
    [4, 8, 12, 16]
])

print (arr[[0, 2], [3, 1]]) # [4 6]
```
以上面这个例子来说，其含义是: 选择第一行和第三行，然后对第一行选择第四列，对第三行选择第二列。

boolean/mask index

所谓 boolean index，就是用一个由 boolean 类型值组成的数组来选择元素的方法。比如说对下面这样多维数组。如果要取其中 值大于 5 的元素，就可以用上 boolean index 了，如下所示:

import numpy as np

arr = np.array([[1, 2, 3, 4],
                [2, 4, 6, 8],
                [3, 6, 9, 12],
                [4, 8, 12, 16]])
mask = arr > 5

print('boolean mask is:',mask)
print('-------------')
print (arr[mask])

"""
boolean mask is: [[False False False False]
 [False False  True  True]
 [False  True  True  True]
 [False  True  True  True]]
-------------
[ 6  8  6  9 12  8 12 16]
"""

除了比较运算能产生 boolean mask 数组以外， Numpy 本身也提供了一些工具方法:

numpy.iscomplex
numpy.isreal
numpy.isfinite
numpy.isinf
numpy.isnan

切片和索引的同异

切片和索引都是访问多维数组中元素的方法，这是两者的共同点，不同之处有:
1. 切片得到的是原多维数组的一个 视图(view) ，修改切片中的内容会导致原多维数组的内容也发生变化
2. 切片得到在多维数组中连续(或按特定步长连续)排列的值，而索引可以得到任意位置的值，自由度更大一些
不考虑第一点的话，切片的操作是可以用索引操作来实现的，不过这没有必要就是了。

对于第一点，见下面的实验:
```
import numpy as np

arr = np.arange(12).reshape(2, 6)
print ('array is:',arr)

'''
array is:
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]
'''

slc = arr[:, 2:5]
print ('slice is:',slc)

"""
slice is:
[[ 2  3  4]
 [ 8  9 10]]
 """

slc[1, 2] = 10000
print('modified slice is:',slc)

'''
modified slice is:
[[    2     3     4]
 [    8     9 10000]]'
'''
print ('array is now:',arr)
"""
array is now:
[[    0     1     2     3     4     5]
 [    6     7     8     9 10000    11]]
"""
```

扩展1–区分NumPy中的随机函数

在NumPy中，有几个用于生成随机数的函数，它们分别是np.random.randn()、np.random.rand()、 np.random.random()和np.random.randint()。虽然这些函数都用于生成随机数，但它们之间有着明显的区别8-11。

np.random.randn()

np.random.randn()函数用于生成服从标准正态分布的随机数。标准正态分布，也称为高斯分布，是一种概率分布，其概率密度函数呈钟形曲线，均值为0，标准差为1，np.random.randn()函数可以生成一维或多维的数组，数组的形状由传入的参数决定。

例如，np.random.randn(3, 4)将生成一个3行4列的二维数组，数组中的每个元素都是从标准正态分布中随机抽取的。

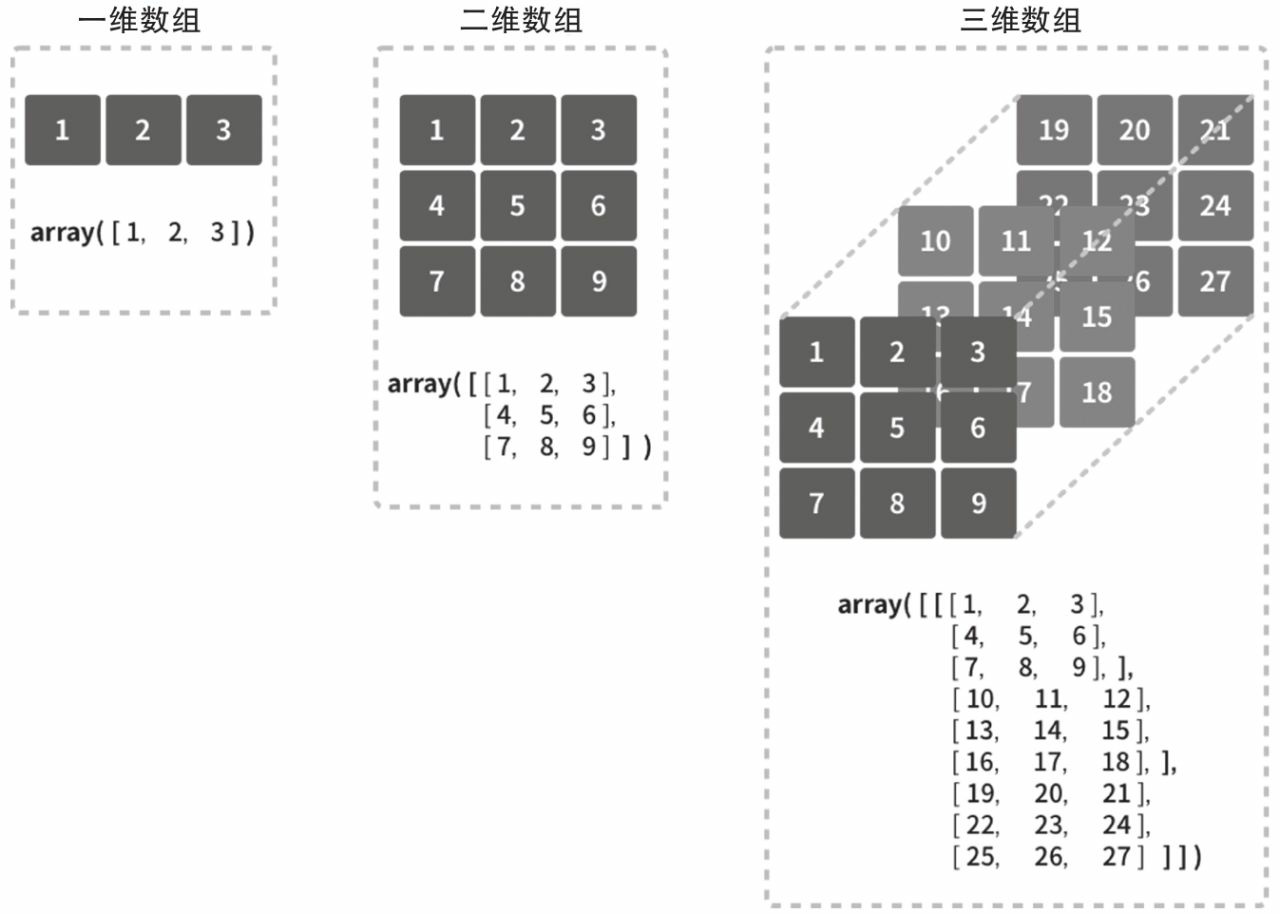
均匀分布:
也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。
均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为U（a，b）。
均匀分布的概率密度函数为：

arr1=np.random.randn(2,4)  #二行四列，或者说一维大小为2，二维大小为4
#均值为0，方差为1
print(arr1)
print(type(arr1)) #<class 'numpy.ndarray'>
 
arr2=np.random.rand()
print(arr2) #0.37338593251088137
print(type(arr2))  #<class 'float'>
 
  
"""
结果如下：
[[ 0.55364415 -0.37297911  1.73028369 -0.80407509]
 [-1.15456845 -0.71088324  0.42676781  0.30948302]]
<class 'numpy.ndarray'>
0.8751684387697356
<class 'float'>
"""

指定数学期望和方差的正态分布

#Two-by-four array of samples from N(3, 6.25):
arr3=2.5 * np.random.randn(2,4)+3  #2.5是标准差，3是期望
print(arr3)
 
'''
结果如下：
[[0.9590157  1.78262269 1.97589322 3.5793825 ]
 [2.72009412 4.38595686 4.45418161 6.97061624]]
'''

np.random.rand()

np.random.rand()函数用于生成[0, 1)区间内的均匀分布的随机数，以float形式返回。这个函数也可以生成一维或多维的数组，数组的形状由传入的参数决定。

例如，np.random.rand(3, 4)将生成一个3行4列的二维数组，数组中的每个元素都是在[0, 1)区间内随机生成的。

np.random.random()

np.random.random()函数与np.random.rand()函数在功能上是相同的，都是用于生成[0, 1)区间内的均匀分布的随机数。这两个函数可以互换使用，没有本质的区别。相同点：两个函数都是在 [0, 1) 的均匀分布中产生随机数。不同点：参数传递不同。random.random( )接收一个单独的元组，而random.rand( )接收分开的参数

例如：

要生成3行5列的数组，你可以

np.random.rand(3, 5)

或者

np.random.random((3, 5))

这边需要注意的是这个函数的参数，只有一个参数“size”，有三种取值，None，int型整数，或者int型元组。

而在之前的numpy.random.rand()中可以有多个参数。

比方说，如果我们要产生一个2*4的随机数组(不考虑服从什么分布)，那么在rand中的写法是：numpy.random.rand(2,4)，而在random中的写法是numpy.random.random( (2,4) )，这里面是个元组，是有小括弧的。

np.random.random_sample()

返回半开区间 [0.0, 1.0) 内的随机浮点数。结果来自于“连续均匀”分布规定的间隔。来样 Unif[a,b),b>a 乘 random_sample的输出由*(ba)*并添加：

(b - a) * random_sample() + a

参数：int 或 int 元组，可选。输出形状。例如，如果给定形状是(m, n, k) ，则抽取m * n * k样本。默认值为 None，在这种情况下返回单个值。

输出：形状size的随机浮点数数组（除非size=None ，在这种情况下返回单个浮点数）。

random() 、 ranf()和sample()都是random_sample()的别名[8]。

np.random.randint()

参数：randint(low, high=None, size=None, dtype=‘l’)

其中low是整型元素，表示范围的下限，可以取到。high表示范围的上限，不能取到。也就是左闭右开区间。high没有填写时，默认生成随机数的范围是[0，low)

size可以是int整数，或者int型的元组，表示产生随机数的个数，或者随机数组的形状。

dtype表示具体随机数的类型，默认是int，可以指定成int64[9]。

#产生一个[0,10)之间的随机整数
temp1=np.random.randint(10)
print(temp1)
print(type(temp1))  #<class 'int'>
 
'''
5
<class 'int'>
'''


temp2=np.random.randint(10,dtype="int64")
print(type(temp2))
 
'''
<class 'numpy.int64'>
'''


#产生[0,10)之间的随机整数8个，以数组的形式返回
temp3=np.random.randint(10,size=8)
print(temp3)
'''
[6 6 0 3 4 2 5 3]
'''
 
temp4=np.random.randint(10,size=(2,4))
print(temp4)
'''
[[7 5 4 5]
 [5 2 7 6]]
'''

temp5=np.random.randint(5,10,size=(2,4))
print(temp5)
 
'''
[[8 5 8 6]
 [9 8 6 9]]
'''

总结

这三个函数的主要区别在于它们生成的随机数的分布类型不同：

np.random.randn()生成服从标准正态分布的随机数；
np.random.rand()和np.random.random()生成[0, 1)区间内的均匀分布的随机数。

在实际应用中，我们需要根据具体的需求选择合适的函数来生成随机数。例如，如果我们需要模拟一个自然现象，其分布符合正态分布，那么就应该使用np.random.randn()；如果我们需要生成一个在[0, 1)区间内的随机概率值，那么就可以使用np.random.rand()或np.random.random()。

最后，需要注意的是，由于这些函数都是基于随机数生成器，所以每次运行代码时生成的随机数可能会有所不同。如果需要得到可复现的结果，可以在代码开始处设置随机数种子，例如使用np.random.seed(0)。

以上就是关于NumPy中np.random.randn(), np.random.rand(), 和 np.random.random()这三个函数的详细解释和比较。希望能够帮助读者更好地理解和使用这些函数。

图示

np.random.rand 用于均匀分布（在半开区间 [0.0, 1.0) ）

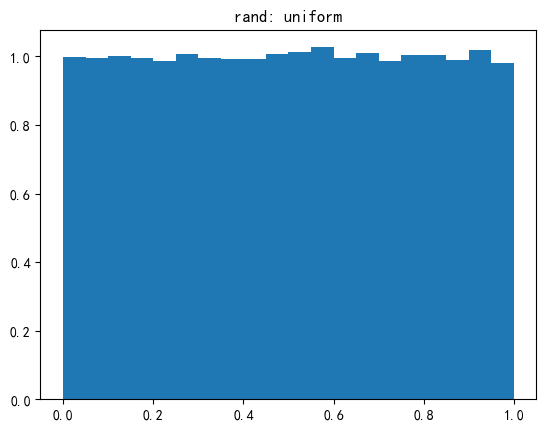
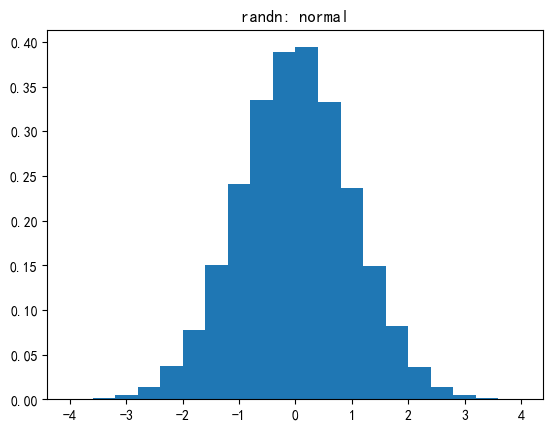
np.random.randn 用于标准正态（又名高斯）分布（均值为 0，方差为 1）12

import numpy as np
import matplotlib.pyplot as plt

sample_size = 100000
uniform = np.random.rand(sample_size)
normal = np.random.randn(sample_size)

pdf, bins, patches = plt.hist(uniform, bins=20, range=(0, 1), density=True)
plt.title('rand: uniform')
plt.show()

pdf, bins, patches = plt.hist(normal, bins=20, range=(-4, 4), density=True)
plt.title('randn: normal')
plt.show()

扩展2–NumPy 的回顾与生态

论文地址：https://www.nature.com/articles/s41586-020-2649-2

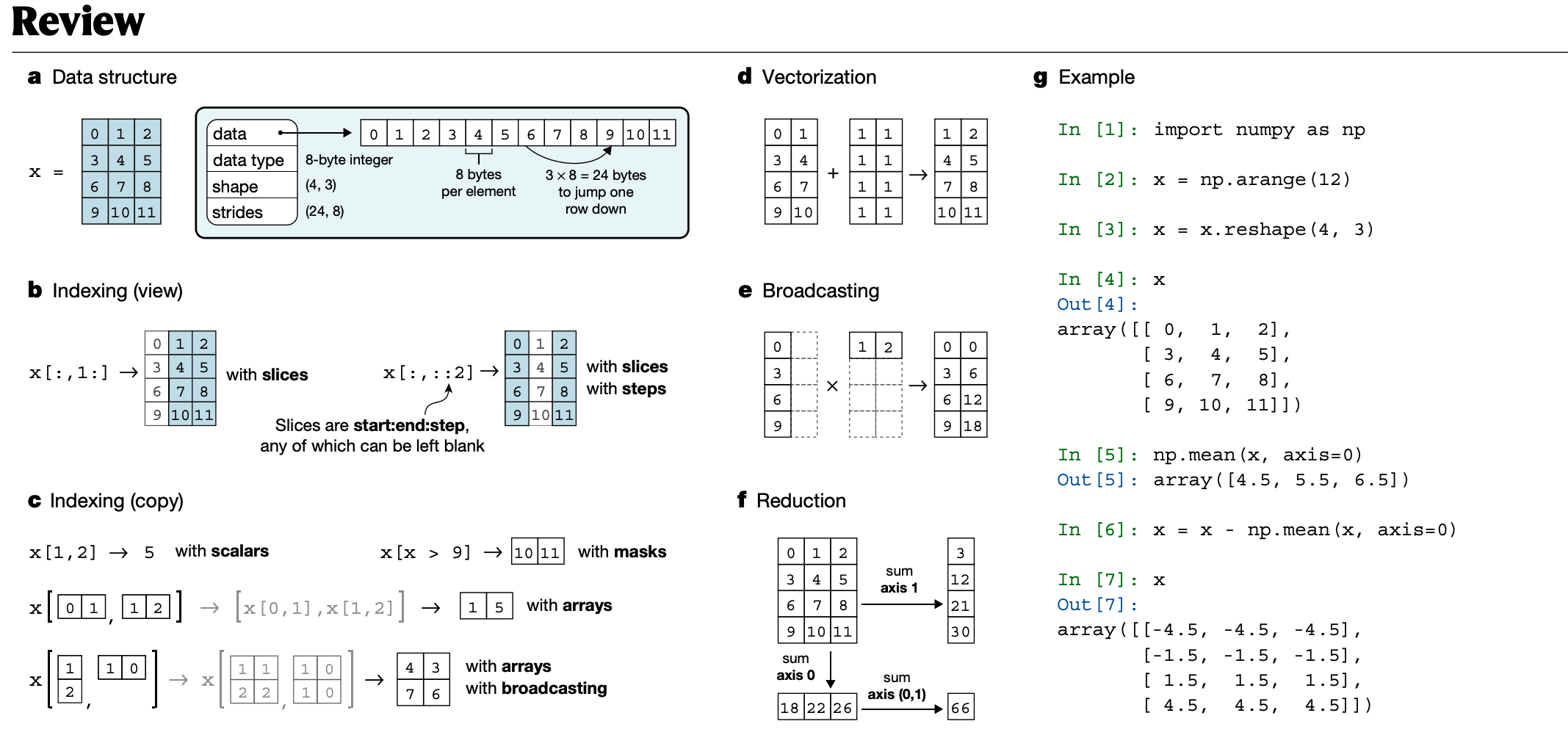
a ，NumPy 数组数据结构及其关联的元数据字段。 b ，使用切片和步骤对数组进行索引。这些操作返回原始数据的“视图”。 c ，使用掩码、标量坐标或其他数组对数组进行索引，以便它返回原始数据的“副本”。在下面的示例中，一个数组与其他数组一起索引；这会在执行查找之前广播索引参数。 d ，矢量化有效地将操作应用于元素组。 e 、二维数组乘法中的广播。 f ，归约运算沿一个或多个轴起作用。在此示例中，数组沿选择的轴求和以生成向量，或沿两个轴连续求和以生成标量。 g ，示例 NumPy 代码，说明其中一些概念。

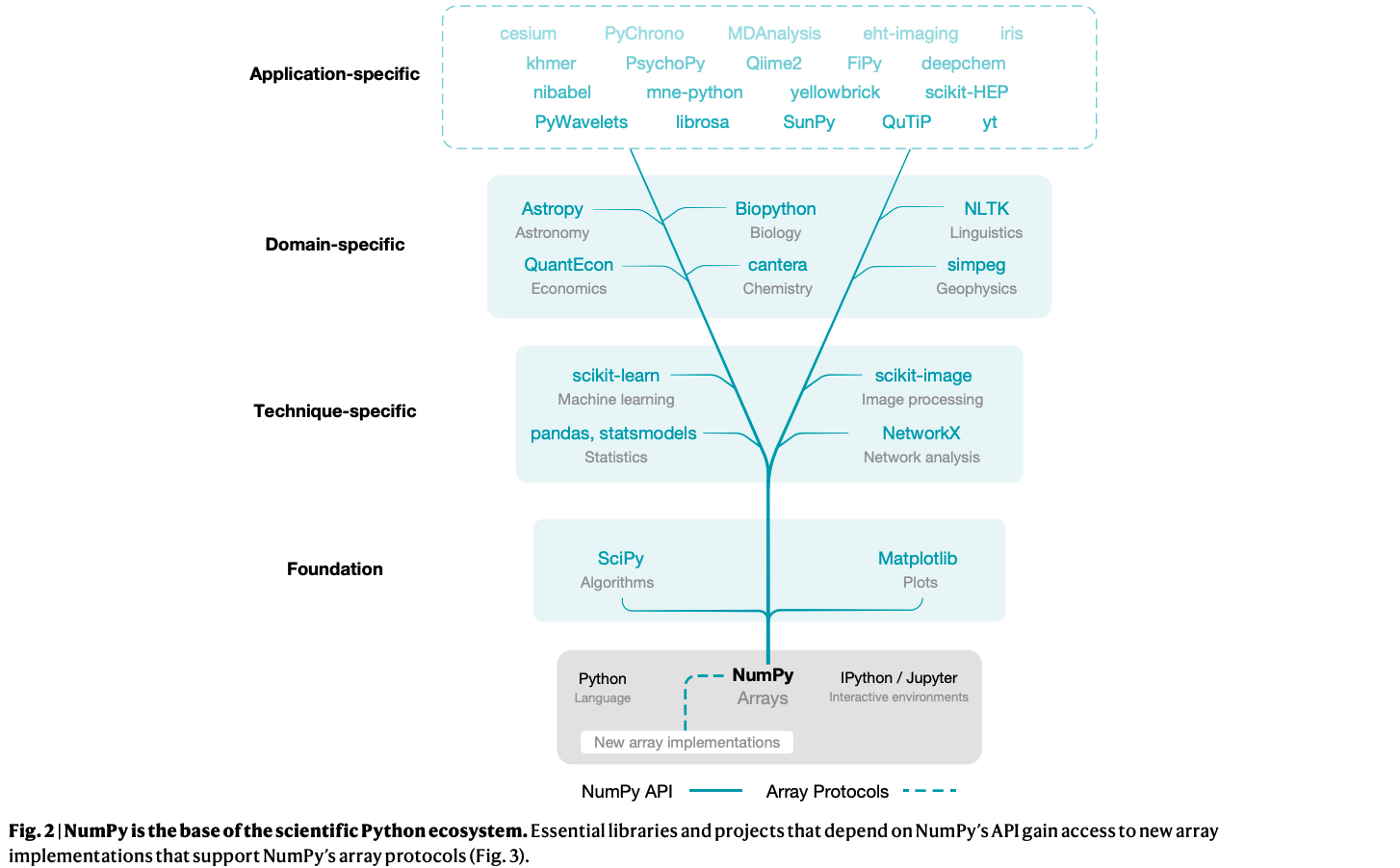
NumPy 是科学 Python 生态系统的基础。依赖于 NumPy API 的基本库和项目可以访问支持 NumPy 数组协议的新数组实现。

其他可以看看参考18-25。

参考：

[1] https://gairuo.com/p/numpy-glance
[2] https://pydata.readthedocs.io/zh/latest/ch04/p01_the_numpy_ndarray_a_multidimensional_array_object.html#ndarray
[3] https://juejin.cn/post/7367753873892704275
[4] https://www.sharpsightlabs.com/blog/numpy-axes-explained/
[5] https://www.showmeai.tech/article-detail/143
[6] https://www.hello-algo.com/chapter_array_and_linkedlist/
[7] https://www.zmonster.me/2016/03/09/numpy-slicing-and-indexing.html
[8] https://cloud.baidu.com/article/3300680
[9] https://www.yutaka-note.com/entry/numpy_random
[10] https://blog.csdn.net/sinat_28576553/article/details/82926047
[11] https://segmentfault.com/q/1010000043236342
[12] https://zh.wikipedia.org/zh-hans/%E6%A0%87%E9%87%8F_(%E6%95%B0%E5%AD%A6)
[13] https://numpy.org/doc/stable/reference/arrays.scalars.html
[14] https://blog.csdn.net/m0_51775098/article/details/138819711
[15] https://datawhalechina.github.io/thorough-pytorch/%E7%AC%AC%E4%BA%8C%E7%AB%A0/2.1%20%E5%BC%A0%E9%87%8F.html
[16] https://yangwenzhuo.top/2020/02/13/Numpy%E4%B8%AD%E7%9A%84%E5%90%91%E9%87%8F/
[17] https://easyai.tech/ai-definition/tensor/
[18] https://blog.51cto.com/u_15127602/4670535
[19] https://pyda.cc/docs/Python-Data-Analysis-Chapter-04/
[20] https://www.hello-algo.com/chapter_array_and_linkedlist/
[21] https://m.thepaper.cn/baijiahao_10641437
[22] https://numpy123.com/article/basics/numpy_matrices_vectors/
[24] https://mp.weixin.qq.com/s/FOKiJrYl7z8g7VG8z-HsTw
[25] https://www.labri.fr/perso/nrougier/from-python-to-numpy/