leetcode-数组篇7
leetcode-303
给定一个整数数组
nums,处理以下类型的多个查询:
- 计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right实现
NumArray类:
NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])示例 1:
输入: ["NumArray", "sumRange", "sumRange", "sumRange"] [[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]] 输出: [null, 1, -1, -3] 解释: NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]); numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3) numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))提示:
1 <= nums.length <= 104-105 <= nums[i] <= 1050 <= i <= j < nums.length- 最多调用
104次sumRange方法
思路:题目很简单,一看就是前缀和的题目,类似的题目还有leetcode560等题目
每个位置保存自身及前面所有数的和就行,求某个区间段直接减一下就出来了
class NumArray {
vector<int> vec;
public:
NumArray(vector<int>& nums) {
int sum = 0;
for (auto num : nums) {
sum += num;
vec.push_back(sum);
}
}
int sumRange(int left, int right) {
if (left == 0) {
return vec[right];
}
return vec[right] - vec[left - 1];
}
};
/**
* Your NumArray object will be instantiated and called as such:
* NumArray* obj = new NumArray(nums);
* int param_1 = obj->sumRange(left,right);
*/leetcode-304
给定一个二维矩阵
matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。实现
NumMatrix类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。示例 1:
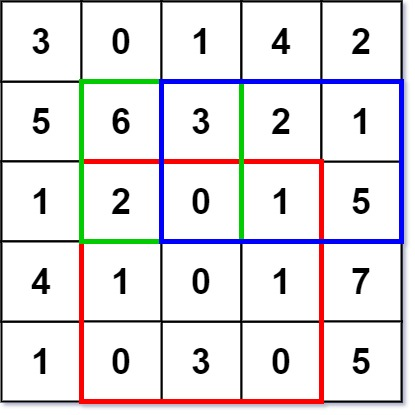
输入: ["NumMatrix","sumRegion","sumRegion","sumRegion"] [[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]] 输出: [null, 8, 11, 12] 解释: NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]); numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和) numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和) numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200-105 <= matrix[i][j] <= 1050 <= row1 <= row2 < m0 <= col1 <= col2 < n- 最多调用
104次sumRegion方法
思路:刚才题目的升级版(当然也可以用上一题的方法做,不过这样get不到该题目的核心)
上一个题目中,我们在每个位置保存该位置及之前所有数的和
这一题目中,我们每个节点保存该位置及左上方所有数的和,这样右下角的点减去其他几个点,就得到了四个点围成的区域的和
class NumMatrix {
vector<vector<int>>vec;
public:
NumMatrix(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
vec.resize(m, vector<int>(n, 0));
for(int i=0; i<matrix.size(); i++) {
for(int j=0; j<matrix[0].size(); j++) {
int sum = 0;
sum += i>0 ? vec[i-1][j] : 0;
sum += j>0 ? vec[i][j-1] : 0;
sum += matrix[i][j];
if(i > 0 && j > 0) {
sum -= vec[i-1][j-1];
}
vec[i][j] = sum;
}
}
}
int sumRegion(int row1, int col1, int row2, int col2) {
int sum = 0;
if(row1 == 0 && col1 == 0) {
return vec[row2][col2];
} else if(row1 == 0) {
return vec[row2][col2] - vec[row2][col1-1];
} else if(col1 == 0) {
return vec[row2][col2] - vec[row1-1][col2];
} else {
return vec[row2][col2] - vec[row2][col1-1] - vec[row1-1][col2] + vec[row1-1][col1-1];
}
}
};
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix* obj = new NumMatrix(matrix);
* int param_1 = obj->sumRegion(row1,col1,row2,col2);
*/leetcode-238
给你一个整数数组
nums,返回 数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。题目数据 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请 不要使用除法,且在
O(n)时间复杂度内完成此题。示例 1:
输入: nums =[1,2,3,4]输出:[24,12,8,6]示例 2:
输入: nums = [-1,1,0,-3,3] 输出: [0,0,9,0,0]提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内进阶:你可以在
O(1)的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
思路:这个题目很有意思,做过的人一眼就知道怎么做了,没做过的可能要想半天
其实就是从左往右,记录每个数左边的乘积,再从右往左,记录每个数右边的乘积
乘起来就是答案
重点是答案怎么压缩到一个数组里面
PS:类似的题目还有leetcode上的分糖果等题目,需要左右各遍历一遍
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
vector<int>res(nums.size(), 0);
res[0] = 1;
for(int i=1; i<nums.size(); i++) {
res[i] = res[i-1]*nums[i-1];
}
int r = 1;
for(int i=nums.size()-1; i>=0; i--) {
res[i] *= r;
r *= nums[i];
}
return res;
}
};