python机器学习课程——决策树全网最详解超详细笔记附代码
文章目录
- 决策树算法
- 一、简介
- 1.概述
- 2.决策树学习
- 3.典型算法
- 4.基本思想
- 5.构造方法
- 6.基本算法
- 二、ID3决策树
- 1、信息熵
- 2、条件熵
- 3、信息增益
- 4、总结
- 5、决策树进行分类的步骤
- 三、ID3决策树示例
- 1、数据集
- 2、计算经验熵(香农熵)
- 3、计算信息增益
- 4、树的生成
- 5、树的深度和广度计算
- 6、未知数据的预测
- 7、树的存储与读取(以二进制形式存储)
- 8、完整代码
- 四、C4.5决策树
- 信息增益
- 五、CART决策树
- 基尼指数
- 六、连续值与缺失值的处理
- 1.连续值处理
- 2.缺失值处理
- 七、CART分类树示例
- 1.数据集
- 2.引入要用到的包
- 3.读入数据集
- 4.计算Gini指数
- 5.取得节点划分的属性
- 6.树节点
- 7.树的生成
- 8.树的遍历
- 9.预测
- 10.计算准确率
- 11.完整代码
- 八、CART回归树
- 1.原理分析
- 2.数据集
- 3. 引入要用的包
- 4.数据集的读取和处理
- 5.area与特征值分离
- 6.误差计算
- 7.划分节点的数据与特征的获取
- 8.树结点
- 9.叶子节点回归值的计算
- 10.生成树
- 11.树的遍历
- 12.预测
- 13.“链表”式树转化为字典树
- 14.树的可视化
- 15.完整代码
- 九、剪枝
决策树算法
一、简介
1.概述
决策树算法是一种逼近离散函数值的方法。它是一种典型的分类方法,首先对数据进行处理,利用归纳算法生成可读的规则和决策树,然后使用决策对新数据进行分析。本质上决策树是通过一系列规则对数据进行分类的过程。
决策树方法最早产生于上世纪60年代,到70年代末。由J Ross Quinlan提出了ID3算法,此算法的目的在于减少树的深度。但是忽略了叶子数目的研究。C4.5算法在ID3算法的基础上进行了改进,对于预测变量的缺值处理、剪枝技术、派生规则等方面作了较大改进,既适合于分类问题,又适合于回归问题。
决策树算法构造决策树来发现数据中蕴涵的分类规则.如何构造精度高、规模小的决策树是决策树算法的核心内容。决策树构造可以分两步进行。第一步,决策树的生成:由训练样本集生成决策树的过程。一般情况下,训练样本数据集是根据实际需要有历史的、有一定综合程度的,用于数据分析处理的数据集。第二步,决策树的剪枝:决策树的剪枝是对上一阶段生成的决策树进行检验、校正和修下的过程,主要是用新的样本数据集(称为测试数据集)中的数据校验决策树生成过程中产生的初步规则,将那些影响预衡准确性的分枝剪除。
2.决策树学习
目标:根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确的分类。决策树学习本质上是从训练数据集中归纳出一组分类规则。能对训练数据进行正确分类的决策树可能有多个,可能没有。在选择决策树时,应选择一个与训练数据矛盾较小的决策树,同时具有很好的泛化能力;而且选择的条件概率模型应该不仅对训练数据有很好的拟合,而且对未知数据有很好的预测。
损失函数:通常是正则化的极大似然函数
策略:是以损失函数为目标函数的最小化
因为从所有可能的决策树中选取最优决策树是NP完全问题,所以现实中决策树学习通常采用启发式方法,近似求解这一最优化问题,得到的决策树是次最优(sub-optimal)的。
决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得对各个子数据集有一个最好的分类的过程。包含特征选择、决策树的生成和决策树的剪枝过程。
剪枝:
目的:将树变得更简单,从而使它具有更好的泛化能力。
步骤:去掉过于细分的叶结点,使其回退到父结点,甚至更高的结点,然后将父结点或更高的结点改为新的叶结点。
决策树的生成对应模型的局部选择,决策树的剪枝对应于模型的全局选择。决策树的生成只考虑局部最优,决策树的剪枝则考虑全局最优。
特征选择:
如果特征数量很多,在决策树学习开始时对特征进行选择,只留下对训练数据有足够分类能力的特征。(例如把名字不作为一个特征进行选择)
3.典型算法
决策树的典型算法有ID3,C4.5,CART等。
国际权威的学术组织,数据挖掘国际会议ICDM (the IEEE International Conference on Data Mining)在2006年12月评选出了数据挖掘领域的十大经典算法中,C4.5算法排名第一。C4.5算法是机器学习算法中的一种分类决策树算法,其核心算法是ID3算法。C4.5算法产生的分类规则易于理解,准确率较高。不过在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,在实际应用中因而会导致算法的低效。
决策树算法的优点如下:
(1)分类精度高;
(2)生成的模式简单;
(3)对噪声数据有很好的健壮性。
因而是目前应用最为广泛的归纳推理算法之一,在数据挖掘中受到研究者的广泛关注。
4.基本思想
1)树以代表训练样本的单个结点开始。
2)如果样本都在同一个类.则该结点成为树叶,并用该类标记。
3)否则,算法选择最有分类能力的属性作为决策树的当前结点.
4)根据当前决策结点属性取值的不同,将训练样本数据集tlI分为若干子集,每个取值形成一个分枝,有几个取值形成几个分枝。匀针对上一步得到的一个子集,重复进行先前步骤,递4’I形成每个划分样本上的决策树。一旦一个属性出现在一个结点上,就不必在该结点的任何后代考虑它。
5)递归划分步骤仅当下列条件之一成立时停止:
①给定结点的所有样本属于同一类。
②没有剩余属性可以用来进一步划分样本.在这种情况下.使用多数表决,将给定的结点转换成树叶,并以样本中元组个数最多的类别作为类别标记,同时也可以存放该结点样本的类别分布,
③如果某一分枝tc,没有满足该分支中已有分类的样本,则以样本的多数类创建一个树叶。 [3]
5.构造方法
决策树构造的输入是一组带有类别标记的例子,构造的结果是一棵二叉树或多叉树。二叉树的内部节点(非叶子节点)一般表示为一个逻辑判断,如形式为a=aj的逻辑判断,其中a是属性,aj是该属性的所有取值:树的边是逻辑判断的分支结果。多叉树(ID3)的内部结点是属性,边是该属性的所有取值,有几个属性值就有几条边。树的叶子节点都是类别标记。 [3]
由于数据表示不当、有噪声或者由于决策树生成时产生重复的子树等原因,都会造成产生的决策树过大。因此,简化决策树是一个不可缺少的环节。寻找一棵最优决策树,主要应解决以下3个最优化问题:①生成最少数目的叶子节点;②生成的每个叶子节点的深度最小;③生成的决策树叶子节点最少且每个叶子节点的深度最小。
6.基本算法

二、ID3决策树
ID3算法是决策树的一种,它是基于奥卡姆剃刀原理的,即用尽量用较少的东西做更多的事。ID3算法,即Iterative Dichotomiser 3,迭代二叉树3代,是Ross Quinlan发明的一种决策树算法,这个算法的基础就是上面提到的奥卡姆剃刀原理,越是小型的决策树越优于大的决策树,尽管如此,也不总是生成最小的树型结构,而是一个启发式算法。
在信息论中,期望信息越小,那么信息增益就越大,从而纯度就越高。ID3算法的核心思想就是以信息增益来度量属性的选择,选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜搜索历可能的决策空间。
1、信息熵
熵(entropy)表示随机变量不确定性的度量,也就是熵越大,变量的不确定性就越大。设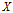 是一个有限值的离散随机变量,其概率分布为:
是一个有限值的离散随机变量,其概率分布为:
P
(
X
=
x
i
)
=
p
i
,
i
=
1
,
2
,
…
,
n
P(X = x_i) = p_i , i = 1,2,…,n
P(X=xi)=pi,i=1,2,…,n
则随机变量X的熵定义为:
H
(
X
)
=
−
∑
i
=
1
n
l
o
g
2
p
i
(
若
p
i
=
0
,
定义
0
l
o
g
0
=
0
)
H(X) = - \sum_{i = 1}^{n} {log_2 p_i} (若p_i = 0,定义 0log0 = 0)
H(X)=−i=1∑nlog2pi(若pi=0,定义0log0=0)
2、条件熵
条件熵H(Y|X)表示在已知随机变量X条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵为:
H
(
Y
∣
X
)
=
∑
i
=
1
n
p
i
H
(
Y
∣
X
=
x
i
)
,
p
i
=
P
(
X
=
x
i
)
H(Y|X) = \sum_{i = 1}^{n}{p_i H(Y|X = x_i)} , p_i = P(X = x_i)
H(Y∣X)=i=1∑npiH(Y∣X=xi),pi=P(X=xi)
3、信息增益
特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即:
g
(
D
,
A
)
=
H
(
D
)
−
H
(
D
∣
A
)
g(D,A) = H(D) - H(D|A)
g(D,A)=H(D)−H(D∣A)
信息增益大的特征具有更强的分类能力
4、总结
给定训练数据集D和特征A:
经验熵H(D)表示对数据集D进行分类的不确定性
经验条件熵H(D|A)表示在特征A给定的条件下对数据集D进行分类的不确定性
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A) = H(D) - H(D|A) g(D,A)=H(D)−H(D∣A)表示由于特征A而使得对数据 D的分类的不确定性减少的程度。
5、决策树进行分类的步骤
-
利用样本数据集构造一颗决策树,并通过构造的决策树建立相应的分类模型。这个过程实际上是从一个数据中获取知识,进行规制提炼的过程。
-
利用已经建立完成的决策树模型对数据集进行分类。即对未知的数据集元组从根节点依次进行决策树的游历,通过一定的路径游历至某叶子节点,从而找到该数据元组所在的类或类的分布。
三、ID3决策树示例
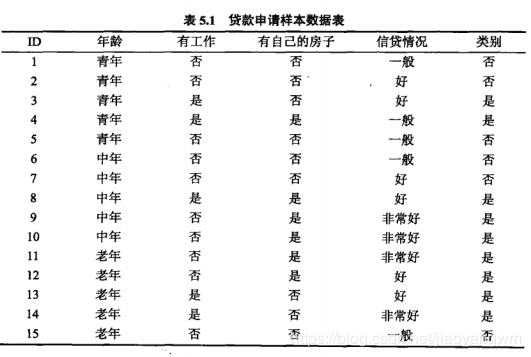
在编写代码之前,我们先对数据集进行属性标注。
- 年龄:0代表青年,1代表中年,2代表老年;
- 有工作:0代表否,1代表是;
- 有自己的房子:0代表否,1代表是;
- 信贷情况:0代表一般,1代表好,2代表非常好;
- 类别(是否给贷款):no代表否,yes代表是。
1、数据集
dataSet=[[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels=['年龄','有工作','有自己的房子','信贷情况']
2、计算经验熵(香农熵)
P ( X = x i ) = p i , i = 1 , 2 , … , n P(X = x_i) = p_i , i = 1,2,…,n P(X=xi)=pi,i=1,2,…,n
H ( X ) = − ∑ i = 1 n l o g 2 p i ( 若 p i = 0 , 定义 0 l o g 0 = 0 ) H(X) = - \sum_{i = 1}^{n} {log_2 p_i} (若p_i = 0,定义 0log0 = 0) H(X)=−i=1∑nlog2pi(若pi=0,定义0log0=0)
from math import log
def calcShannonEnt(dataSet):
# 统计数据数量
numEntries = len(dataSet)
# 存储每个label出现次数
label_counts = {}
# 统计label出现次数
for featVec in dataSet:
current_label = featVec[-1]
if current_label not in label_counts: # 提取label信息
label_counts[current_label] = 0 # 如果label未在dict中则加入
label_counts[current_label] += 1 # label计数
shannon_ent = 0 # 经验熵
# 计算经验熵
for key in label_counts:
prob = float(label_counts[key]) / numEntries
shannon_ent -= prob * log(prob, 2)
return shannon_ent
# 运行结果
# 0.9709505944546686
3、计算信息增益
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A) = H(D) - H(D|A) g(D,A)=H(D)−H(D∣A)
def splitDataSet(data_set, axis, value):
ret_dataset = []
for feat_vec in data_set:
if feat_vec[axis] == value:
reduced_feat_vec = feat_vec[:axis]
reduced_feat_vec.extend(feat_vec[axis + 1:])
ret_dataset.append(reduced_feat_vec)
return ret_dataset
def chooseBestFeatureToSplit(dataSet):
# 特征数量
num_features = len(dataSet[0]) - 1
# 计算数据香农熵
base_entropy = calcShannonEnt(dataSet)
# 信息增益
best_info_gain = 0.0
# 最优特征索引值
best_feature = -1
# 遍历所有特征
for i in range(num_features):
# 获取dataset第i个特征
feat_list = [exampel[i] for exampel in dataSet]
# 创建set集合,元素不可重合
unique_val = set(feat_list)
# 经验条件熵
new_entropy = 0.0
# 计算信息增益
for value in unique_val:
# sub_dataset划分后的子集
sub_dataset = splitDataSet(dataSet, i, value)
# 计算子集的概率
prob = len(sub_dataset) / float(len(dataSet))
# 计算经验条件熵
new_entropy += prob * calcShannonEnt(sub_dataset)
# 信息增益
info_gain = base_entropy - new_entropy
# 打印每个特征的信息增益
print("第%d个特征的信息增益为%.3f" % (i, info_gain))
# 计算信息增益
if info_gain > best_info_gain:
# 更新信息增益
best_info_gain = info_gain
# 记录信息增益最大的特征的索引值
best_feature = i
print("最优索引值:" + str(best_feature))
print()
return best_feature
# 运行结果
# 第0个特征的信息增益为0.083
# 第1个特征的信息增益为0.324
# 第2个特征的信息增益为0.420
# 第3个特征的信息增益为0.363
# 最优索引值:2
4、树的生成
import operator
def majority_cnt(class_list):
class_count = {}
# 统计class_list中每个元素出现的次数
for vote in class_list:
if vote not in class_count:
class_count[vote] = 0
class_count[vote] += 1
# 根据字典的值降序排列
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0]
def creat_tree(dataSet, labels, featLabels):
# 取分类标签(是否放贷:yes or no)
class_list = [exampel[-1] for exampel in dataSet]
# 如果类别完全相同则停止分类
if class_list.count(class_list[0]) == len(class_list):
return class_list[0]
# 遍历完所有特征时返回出现次数最多的类标签
if len(dataSet[0]) == 1:
return majority_cnt(class_list)
# 选择最优特征
best_feature = chooseBestFeatureToSplit(dataSet)
# 最优特征的标签
best_feature_label = labels[best_feature]
featLabels.append(best_feature_label)
# 根据最优特征的标签生成树
my_tree = {best_feature_label: {}}
# 删除已使用标签
del(labels[best_feature])
# 得到训练集中所有最优特征的属性值
feat_value = [exampel[best_feature] for exampel in dataSet]
# 去掉重复属性值
unique_vls = set(feat_value)
for value in unique_vls:
my_tree[best_feature_label][value] = creat_tree(splitDataSet(dataSet, best_feature, value), labels, featLabels)
return my_tree
# 运行结果
# {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
5、树的深度和广度计算
def get_num_leaves(my_tree):
num_leaves = 0
first_str = next(iter(my_tree))
second_dict = my_tree[first_str]
for key in second_dict.keys():
if type(second_dict[key]).__name__ == 'dict':
num_leaves += get_num_leaves(second_dict[key])
else:
num_leaves += 1
return num_leaves
def get_tree_depth(my_tree):
max_depth = 0 # 初始化决策树深度
firsr_str = next(iter(my_tree)) # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0]
second_dict = my_tree[firsr_str] # 获取下一个字典
for key in second_dict.keys():
if type(second_dict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
this_depth = 1 + get_tree_depth(second_dict[key])
else:
this_depth = 1
if this_depth > max_depth:
max_depth = this_depth # 更新层数
return max_depth
# 运行结果
# 2
# 3
6、未知数据的预测
def classify(input_tree, feat_labels, test_vec):
# 获取决策树节点
first_str = next(iter(input_tree))
# 下一个字典
second_dict = input_tree[first_str]
feat_index = feat_labels.index(first_str)
for key in second_dict.keys():
if test_vec[feat_index] == key:
if type(second_dict[key]).__name__ == 'dict':
class_label = classify(second_dict[key], feat_labels, test_vec)
else:
class_label = second_dict[key]
return class_label
# 测试
testVec = [0, 1, 1, 1]
result = classify(myTree, featLabels, testVec)
if result == 'yes':
print('放贷')
if result == 'no':
print('不放贷')
# 运行结果
# 放贷
7、树的存储与读取(以二进制形式存储)
import pickle
def storeTree(input_tree, filename):
# 存储树
with open(filename, 'wb') as fw:
pickle.dump(input_tree, fw)
def grabTree(filename):
# 读取树
fr = open(filename, 'rb')
return pickle.load(fr)
8、完整代码
from math import log
import operator
import pickle
def calcShannonEnt(dataSet):
# 统计数据数量
numEntries = len(dataSet)
# 存储每个label出现次数
label_counts = {}
# 统计label出现次数
for featVec in dataSet:
current_label = featVec[-1]
if current_label not in label_counts: # 提取label信息
label_counts[current_label] = 0 # 如果label未在dict中则加入
label_counts[current_label] += 1 # label计数
shannon_ent = 0 # 经验熵
# 计算经验熵
for key in label_counts:
prob = float(label_counts[key]) / numEntries
shannon_ent -= prob * log(prob, 2)
return shannon_ent
def splitDataSet(data_set, axis, value):
ret_dataset = []
for feat_vec in data_set:
if feat_vec[axis] == value:
reduced_feat_vec = feat_vec[:axis]
reduced_feat_vec.extend(feat_vec[axis + 1:])
ret_dataset.append(reduced_feat_vec)
return ret_dataset
def chooseBestFeatureToSplit(dataSet):
# 特征数量
num_features = len(dataSet[0]) - 1
# 计算数据香农熵
base_entropy = calcShannonEnt(dataSet)
# 信息增益
best_info_gain = 0.0
# 最优特征索引值
best_feature = -1
# 遍历所有特征
for i in range(num_features):
# 获取dataset第i个特征
feat_list = [exampel[i] for exampel in dataSet]
# 创建set集合,元素不可重合
unique_val = set(feat_list)
# 经验条件熵
new_entropy = 0.0
# 计算信息增益
for value in unique_val:
# sub_dataset划分后的子集
sub_dataset = splitDataSet(dataSet, i, value)
# 计算子集的概率
prob = len(sub_dataset) / float(len(dataSet))
# 计算经验条件熵
new_entropy += prob * calcShannonEnt(sub_dataset)
# 信息增益
info_gain = base_entropy - new_entropy
# 打印每个特征的信息增益
print("第%d个特征的信息增益为%.3f" % (i, info_gain))
# 计算信息增益
if info_gain > best_info_gain:
# 更新信息增益
best_info_gain = info_gain
# 记录信息增益最大的特征的索引值
best_feature = i
print("最优索引值:" + str(best_feature))
print()
return best_feature
def majority_cnt(class_list):
class_count = {}
# 统计class_list中每个元素出现的次数
for vote in class_list:
if vote not in class_count:
class_count[vote] = 0
class_count[vote] += 1
# 根据字典的值降序排列
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0]
def creat_tree(dataSet, labels, featLabels):
# 取分类标签(是否放贷:yes or no)
class_list = [exampel[-1] for exampel in dataSet]
# 如果类别完全相同则停止分类
if class_list.count(class_list[0]) == len(class_list):
return class_list[0]
# 遍历完所有特征时返回出现次数最多的类标签
if len(dataSet[0]) == 1:
return majority_cnt(class_list)
# 选择最优特征
best_feature = chooseBestFeatureToSplit(dataSet)
# 最优特征的标签
best_feature_label = labels[best_feature]
featLabels.append(best_feature_label)
# 根据最优特征的标签生成树
my_tree = {best_feature_label: {}}
# 删除已使用标签
del(labels[best_feature])
# 得到训练集中所有最优特征的属性值
feat_value = [exampel[best_feature] for exampel in dataSet]
# 去掉重复属性值
unique_vls = set(feat_value)
for value in unique_vls:
my_tree[best_feature_label][value] = creat_tree(splitDataSet(dataSet, best_feature, value), labels, featLabels)
return my_tree
def get_num_leaves(my_tree):
num_leaves = 0
first_str = next(iter(my_tree))
second_dict = my_tree[first_str]
for key in second_dict.keys():
if type(second_dict[key]).__name__ == 'dict':
num_leaves += get_num_leaves(second_dict[key])
else:
num_leaves += 1
return num_leaves
def get_tree_depth(my_tree):
max_depth = 0 # 初始化决策树深度
firsr_str = next(iter(my_tree)) # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0]
second_dict = my_tree[firsr_str] # 获取下一个字典
for key in second_dict.keys():
if type(second_dict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
this_depth = 1 + get_tree_depth(second_dict[key])
else:
this_depth = 1
if this_depth > max_depth:
max_depth = this_depth # 更新层数
return max_depth
def classify(input_tree, feat_labels, test_vec):
# 获取决策树节点
first_str = next(iter(input_tree))
# 下一个字典
second_dict = input_tree[first_str]
feat_index = feat_labels.index(first_str)
for key in second_dict.keys():
if test_vec[feat_index] == key:
if type(second_dict[key]).__name__ == 'dict':
class_label = classify(second_dict[key], feat_labels, test_vec)
else:
class_label = second_dict[key]
return class_label
def storeTree(input_tree, filename):
# 存储树
with open(filename, 'wb') as fw:
pickle.dump(input_tree, fw)
def grabTree(filename):
# 读取树
fr = open(filename, 'rb')
return pickle.load(fr)
if __name__ == "__main__":
# 数据集
dataSet = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
# [1, 0, 0, 0, 'yes'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
# 分类属性
labels = ['年龄', '有工作', '有自己的房子', '信贷情况']
print(dataSet)
print()
print(calcShannonEnt(dataSet))
print()
featLabels = []
myTree = creat_tree(dataSet, labels, featLabels)
print(myTree)
print(get_tree_depth(myTree))
print(get_num_leaves(myTree))
#测试数据
testVec = [0, 1, 1, 1]
result = classify(myTree, featLabels, testVec)
if result == 'yes':
print('放贷')
if result == 'no':
print('不放贷')
# 存储树
storeTree(myTree,'classifierStorage.txt')
# 读取树
myTree2 = grabTree('classifierStorage.txt')
print(myTree2)
testVec2 = [1, 0]
result2 = classify(myTree2, featLabels, testVec)
if result2 == 'yes':
print('放贷')
if result2 == 'no':
print('不放贷')
# 运行结果
# [[0, 0, 0, 0, 'no'], [0, 0, 0, 1, 'no'], [0, 1, 0, 1, 'yes'], [0, 1, 1, 0, 'yes'], [0, 0, 0, 0, 'no'], [1, 0, 0, 0, 'no'], [1, 0, 0, 1, 'no'], [1, 1, 1, 1, 'yes'], [1, 0, 1, 2, 'yes'], [1, 0, 1, 2, 'yes'], [2, 0, 1, 2, 'yes'], [2, 0, 1, 1, 'yes'], [2, 1, 0, 1, 'yes'], [2, 1, 0, 2, 'yes'], [2, 0, 0, 0, 'no']]
# 0.9709505944546686
# 第0个特征的信息增益为0.083
# 第1个特征的信息增益为0.324
# 第2个特征的信息增益为0.420
# 第3个特征的信息增益为0.363
# 最优索引值:2
# 第0个特征的信息增益为0.252
# 第1个特征的信息增益为0.918
# 第2个特征的信息增益为0.474
# 最优索引值:1
# {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
# 2
# 3
# 放贷
# {'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
# 放贷
四、C4.5决策树
C4.5决策树实在ID3决策树的基础上进行了优化。将节点的划分标准替换为了信息增益率,能够处理连续值,并且可以处理缺失值,以及能够进行剪枝操作。
信息增益
信息增益率使用“分裂信息”值将信息增益规范化。分类信息类似于Info(D),定义如下:
S
p
l
i
t
I
n
f
o
A
(
D
)
=
−
∑
j
=
1
v
∣
D
j
∣
∣
D
∣
∗
l
o
g
2
(
∣
D
j
∣
∣
D
∣
)
SplitInfo_A(D)=-\sum^{v}_{j=1}\frac{|D_j|}{|D|}*log_2(\frac{|D_j|}{|D|})
SplitInfoA(D)=−j=1∑v∣D∣∣Dj∣∗log2(∣D∣∣Dj∣)
这个值表示通过将训练数据集D划分成对应于属性A测试的v个输出的v个划分产生的信息。信息增益率定义:
G
a
i
n
R
a
t
i
o
(
A
)
=
G
a
i
n
(
A
)
S
p
l
i
t
I
n
f
o
(
a
)
GainRatio(A)=\frac{Gain(A)}{SplitInfo(a)}
GainRatio(A)=SplitInfo(a)Gain(A)
此处的Gain(A)即是前文介绍ID3时的g(D,A)
选择具有最大增益率的属性作为分裂属性。
当属性有很多值时,虽然信息增益变大了,但是相应的属性熵也会变大。所以最终计算的信息增益率并不是很大。在一定程度上可以避免ID3倾向于选择取值较多的属性作为节点的问题。
具体树的构造方法与前文的ID3相同,这里不再赘述
五、CART决策树
CART 树(分类回归树)分为分类树和回归树。顾名思义,分类树用于处理分类问题;回归树用来处理回归问题。我们知道分类和回归是机器学习领域两个重要的方向。分类问题输出特征向量对应的分类结果,回归问题输出特征向量对应的预测值。
分类树和 ID3、C4.5 决策树相似,都用来处理分类问题。不同之处是划分方法。分类树利用基尼指数进行二分。如图所示就是一个分类树。
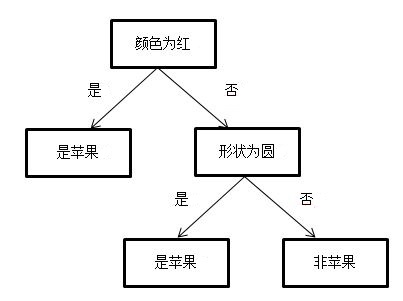
回归树用来处理回归问题。回归将已知数据进行拟合,对于目标变量未知的数据可以预测目标变量的值。如图 所示就是一个回归树,其中 s 是切分点,x 是特征,y 是目标变量。可以看出图 2 利用切分点 s 将特征空间进行划分,y 是在划分单元上的输出值。回归树的关键是如何选择切分点、如何利用切分点划分数据集、如何预测 y 的取值。

基尼指数
数据集D的纯度可以用基尼值来度量:
G
i
n
i
(
D
)
=
∑
k
=
1
∣
y
∣
∑
k
′
≠
k
p
k
p
k
′
=
1
−
∑
k
=
1
∣
y
∣
p
k
2
Gini(D)=\sum^{|y|}_{k=1}\sum_{k'\not=k}p_kp_k'\\ =1-\sum^{|y|}_{k=1}p_k^2
Gini(D)=k=1∑∣y∣k′=k∑pkpk′=1−k=1∑∣y∣pk2
直观来说,Gini(D)反映了从数据集D中随机选取两个样本,其类别标记不一致的概率,因此Gini(D)越小,则数据集D的纯度越高。
属性a的基尼指数定义为
G
i
n
i
_
i
n
d
e
x
(
D
,
a
)
=
∑
V
=
1
V
∣
D
v
∣
∣
D
∣
G
i
n
i
(
D
v
)
Gini\_index(D,a)=\sum^{V}_{V=1}\frac{|D^v|}{|D|}Gini(D^v)
Gini_index(D,a)=V=1∑V∣D∣∣Dv∣Gini(Dv)
于是,我们在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为最优划分属性,即
a
∗
=
a
r
g
m
i
n
G
i
n
i
_
i
n
d
e
x
(
D
,
a
)
,
其中
a
∈
A
a_*= arg\ min\ Gini\_index(D,a),其中a\in A
a∗=arg min Gini_index(D,a),其中a∈A
六、连续值与缺失值的处理
1.连续值处理
由于连续属性的可取值数目不再有限,因此,不能直接根据连续属性的可取值来对结点进行划分.此时,连续属性离散化技术可派上用场.最简单的策略是采用二分法(bi-partition)对连续属性进行处理,这正是C4.5决策树算法中采用的机制[Quinlan, 1993].


后续在cart回归树案例中会有具体代码的展示
2.缺失值处理
由于我没有准备这方面的代码,就在这里分享一个写的极为详细的博客
https://blog.csdn.net/u012328159/article/details/79413610
感兴趣的也可以自己去看瓜书上的讲解
七、CART分类树示例
1.数据集
依旧为上一次用到的Titanic数据集,在此不做过多介绍分析了。
与上次的区别在于为了形成一个二叉树,所有特征离散化后在子叶点分类时只分为了1和非1两类
2.引入要用到的包
import csv
import operator
import copy
import numpy as np
3.读入数据集
def loadDataset(filename):
with open(filename, 'r') as f:
lines = csv.reader(f)
data_set = list(lines)
if filename != 'titanic.csv':
for i in range(len(data_set)):
del(data_set[i][0])
# 整理数据
for i in range(len(data_set)):
del(data_set[i][0])
del(data_set[i][2])
data_set[i][4] += data_set[i][5]
del(data_set[i][5])
del(data_set[i][5])
del(data_set[i][6])
del(data_set[i][-1])
category = data_set[0]
del (data_set[0])
# 转换数据格式
for data in data_set:
data[0] = int(data[0])
data[1] = int(data[1])
if data[3] != '':
data[3] = float(data[3])
else:
data[3] = None
data[4] = float(data[4])
data[5] = float(data[5])
# 补全缺失值 转换记录方式 分类
for data in data_set:
if data[3] is None:
data[3] = 28
# male : 1, female : 0
if data[2] == 'male':
data[2] = 1
else:
data[2] = 0
# age <25 为0, 25<=age<31为1,age>=31为2
if data[3] < 60: # 但是测试得60分界准确率最高???!!!
data[3] = 0
else:
data[3] = 1
# sibsp&parcg以2为界限,小于为0,大于为1
if data[4] < 2:
data[4] = 0
else:
data[4] = 1
# fare以64为界限
if data[-1] < 64:
data[-1] = 0
else:
data[-1] = 1
return data_set, category
4.计算Gini指数
按照公式计算基尼指数
def gini(data, i):
num = len(data)
label_counts = [0, 0, 0, 0]
p_count = [0, 0, 0, 0]
gini_count = [0, 0, 0, 0]
for d in data:
label_counts[d[i]] += 1
for l in range(len(label_counts)):
for d in data:
if label_counts[l] != 0 and d[0] == 1 and d[i] == l:
p_count[l] += 1
print(label_counts)
print(p_count)
for l in range(len(label_counts)):
if label_counts[l] != 0:
gini_count[l] = 2*(p_count[l]/label_counts[l])*(1 - p_count[l]/label_counts[l])
gini_p = 0
for l in range(len(gini_count)):
gini_p += (label_counts[l]/num)*gini_count[l]
print(gini_p)
return gini_p
5.取得节点划分的属性
def get_best_feature(data, category):
if len(category) == 2:
return 1, category[1]
feature_num = len(category) - 1
data_num = len(data)
feature_gini = []
for i in range(1, feature_num+1):
feature_gini.append(gini(data, i))
min = 0
for i in range(len(feature_gini)):
if feature_gini[i] < feature_gini[min]:
min = i
print(feature_gini)
print(category)
print(min+1)
print(category[min+1])
return min+1, category[min + 1]
6.树节点
这里不使用字典建立二叉树(前面ID3用过了),这里自己构建链表式的树
class Node(object):
def __init__(self, item):
self.name = item
self.lchild = None
self.rchild = None
7.树的生成
其中涉及到了预剪枝,后文会再说这个问题
def majority_cnt(class_list):
class_count = {}
# 统计class_list中每个元素出现的次数
for vote in class_list:
if vote not in class_count:
class_count[vote] = 0
class_count[vote] += 1
# 根据字典的值降序排列
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0]
def creat_tree(data, labels, feature_labels=[]):
# 三种结束情况
# 取分类标签(survivor or death)
class_list = [exampel[0] for exampel in data]
if class_list == []:
return Node(0)
# 如果类别完全相同则停止分类
if class_list.count(class_list[0]) == len(class_list):
return Node(class_list[0])
# 遍历完所有特征时返回出现次数最多的类标签
if len(data[0]) == 1:
return Node(majority_cnt(class_list))
# 最优特征的标签
best_feature_num, best_feature_label = get_best_feature(data, labels)
feature_labels.append(best_feature_label)
node = Node(best_feature_label)
ldata = []
rdata = []
for d in data:
if d[best_feature_num] == 1:
del(d[best_feature_num])
ldata.append(d)
else:
del(d[best_feature_num])
rdata.append(d)
labels2 = copy.deepcopy(labels)
del(labels2[best_feature_num])
tree = node
tree.lchild = creat_tree(ldata, labels2, feature_labels)
tree.rchild = creat_tree(rdata, labels2, feature_labels)
return tree
8.树的遍历
def breadth_travel(tree):
"""广度遍历"""
queue = [tree]
while queue:
cur_node = queue.pop(0)
print(cur_node.name, end=" ")
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
print()
9.预测
def prediction(t_tree, test, labels):
result = []
for data in test:
l = copy.deepcopy(labels)
tree = t_tree
for i in range(len(labels)):
if tree.name == 1 or tree.name == 0:
result.append(tree.name)
break
if len(data) == 1:
result.append(0)
break
j = 1
while j < len(data)-1:
if tree.name == l[j]:
break
j += 1
if data[j] == 1:
tree = tree.lchild
else:
tree = tree.rchild
del(l[j])
del(data[j])
return result
10.计算准确率
result = prediction(my_tree, test_set, category)
counts = 0
for i in range(len(test_set)):
if test_set[i][0] == result[i]:
counts += 1
accurancy = counts/len(test_set)
print(accurancy)
11.完整代码
import csv
import operator
import copy
import numpy as np
# 0PassengerId:乘客的ID 不重要
# 1Survived:乘客是否获救,Key:0=没获救,1=已获救
# 2Pclass:乘客船舱等级(1/2/3三个等级舱位)
# 3Name:乘客姓名 不重要
# 4Sex:性别
# 5Age:年龄
# 6SibSp:乘客在船上的兄弟姐妹/配偶数量
# 7Parch:乘客在船上的父母/孩子数量
# 8Ticket:船票号 不重要
# 9Fare:船票价
# 10Cabin:客舱号码 不重要
# 11Embarked:登船的港口 不重要
def loadDataset(filename):
with open(filename, 'r') as f:
lines = csv.reader(f)
data_set = list(lines)
if filename != 'titanic.csv':
for i in range(len(data_set)):
del(data_set[i][0])
# 整理数据
for i in range(len(data_set)):
del(data_set[i][0])
del(data_set[i][2])
data_set[i][4] += data_set[i][5]
del(data_set[i][5])
del(data_set[i][5])
del(data_set[i][6])
del(data_set[i][-1])
category = data_set[0]
del (data_set[0])
# 转换数据格式
for data in data_set:
data[0] = int(data[0])
data[1] = int(data[1])
if data[3] != '':
data[3] = float(data[3])
else:
data[3] = None
data[4] = float(data[4])
data[5] = float(data[5])
# 补全缺失值 转换记录方式 分类
for data in data_set:
if data[3] is None:
data[3] = 28
# male : 1, female : 0
if data[2] == 'male':
data[2] = 1
else:
data[2] = 0
# age <25 为0, 25<=age<31为1,age>=31为2
if data[3] < 60: # 但是测试得60分界准确率最高???!!!
data[3] = 0
else:
data[3] = 1
# sibsp&parcg以2为界限,小于为0,大于为1
if data[4] < 2:
data[4] = 0
else:
data[4] = 1
# fare以64为界限
if data[-1] < 64:
data[-1] = 0
else:
data[-1] = 1
return data_set, category
def gini(data, i):
num = len(data)
label_counts = [0, 0, 0, 0]
p_count = [0, 0, 0, 0]
gini_count = [0, 0, 0, 0]
for d in data:
label_counts[d[i]] += 1
for l in range(len(label_counts)):
for d in data:
if label_counts[l] != 0 and d[0] == 1 and d[i] == l:
p_count[l] += 1
print(label_counts)
print(p_count)
for l in range(len(label_counts)):
if label_counts[l] != 0:
gini_count[l] = 2*(p_count[l]/label_counts[l])*(1 - p_count[l]/label_counts[l])
gini_p = 0
for l in range(len(gini_count)):
gini_p += (label_counts[l]/num)*gini_count[l]
print(gini_p)
return gini_p
def get_best_feature(data, category):
if len(category) == 2:
return 1, category[1]
feature_num = len(category) - 1
data_num = len(data)
feature_gini = []
for i in range(1, feature_num+1):
feature_gini.append(gini(data, i))
min = 0
for i in range(len(feature_gini)):
if feature_gini[i] < feature_gini[min]:
min = i
print(feature_gini)
print(category)
print(min+1)
print(category[min+1])
return min+1, category[min + 1]
def majority_cnt(class_list):
class_count = {}
# 统计class_list中每个元素出现的次数
for vote in class_list:
if vote not in class_count:
class_count[vote] = 0
class_count[vote] += 1
# 根据字典的值降序排列
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0]
class Node(object):
def __init__(self, item):
self.name = item
self.lchild = None
self.rchild = None
def creat_tree(data, labels, feature_labels=[]):
# 三种结束情况
# 取分类标签(survivor or death)
class_list = [exampel[0] for exampel in data]
if class_list == []:
return Node(0)
# 如果类别完全相同则停止分类
if class_list.count(class_list[0]) == len(class_list):
return Node(class_list[0])
# 遍历完所有特征时返回出现次数最多的类标签
if len(data[0]) == 1:
return Node(majority_cnt(class_list))
# 最优特征的标签
best_feature_num, best_feature_label = get_best_feature(data, labels)
feature_labels.append(best_feature_label)
node = Node(best_feature_label)
ldata = []
rdata = []
for d in data:
if d[best_feature_num] == 1:
del(d[best_feature_num])
ldata.append(d)
else:
del(d[best_feature_num])
rdata.append(d)
labels2 = copy.deepcopy(labels)
del(labels2[best_feature_num])
tree = node
tree.lchild = creat_tree(ldata, labels2, feature_labels)
tree.rchild = creat_tree(rdata, labels2, feature_labels)
return tree
def breadth_travel(tree):
"""广度遍历"""
queue = [tree]
while queue:
cur_node = queue.pop(0)
print(cur_node.name, end=" ")
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
print()
def prediction(t_tree, test, labels):
result = []
for data in test:
l = copy.deepcopy(labels)
tree = t_tree
for i in range(len(labels)):
if tree.name == 1 or tree.name == 0:
result.append(tree.name)
break
if len(data) == 1:
result.append(0)
break
j = 1
while j < len(data)-1:
if tree.name == l[j]:
break
j += 1
if data[j] == 1:
tree = tree.lchild
else:
tree = tree.rchild
del(l[j])
del(data[j])
return result
if __name__ == "__main__":
test_set, category = loadDataset('titanic_test.csv')
train_set, category = loadDataset('titanic_train.csv')
print(category)
print(train_set)
print()
print(test_set)
my_tree = creat_tree(train_set, category)
print(my_tree)
breadth_travel(my_tree)
print(category)
print(test_set)
test = copy.deepcopy(test_set)
result = prediction(my_tree, test_set, category)
print(len(test_set))
print(result)
counts = 0
for i in range(len(test_set)):
if test_set[i][0] == result[i]:
counts += 1
print(counts)
accurancy = counts/len(test_set)
print(accurancy)
八、CART回归树
1.原理分析
CART回归树预测回归连续型数据,假设X与Y分别是输入和输出变量,并且Y是连续变量。在训练数据集所在的输入空间中,递归的将每个区域划分为两个子区域并决定每个子区域上的输出值,构建二叉决策树。
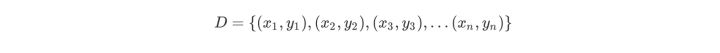
选择最优切分变量j与切分点s:遍历变量j,对规定的切分变量j扫描切分点s,选择使下式得到最小值时的(j,s)对。其中Rm是被划分的输入空间,cm是空间Rm对应的固定输出值。
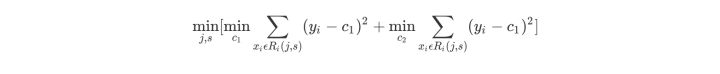
用选定的(j,s)对,划分区域并决定相应的输出值
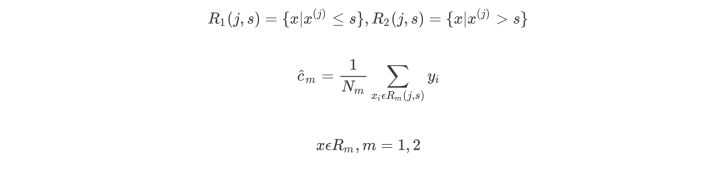
继续对两个子区域调用上述步骤,将输入空间划分为M个区域R1,R2,…,Rm,生成决策树。
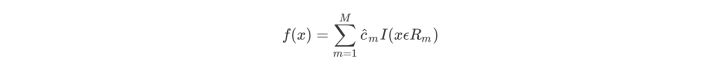
当输入空间划分确定时,可以用平方误差来表示回归树对于训练数据的预测方法,用平方误差最小的准则求解每个单元上的最优输出值。
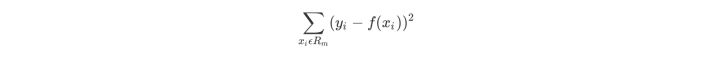
2.数据集
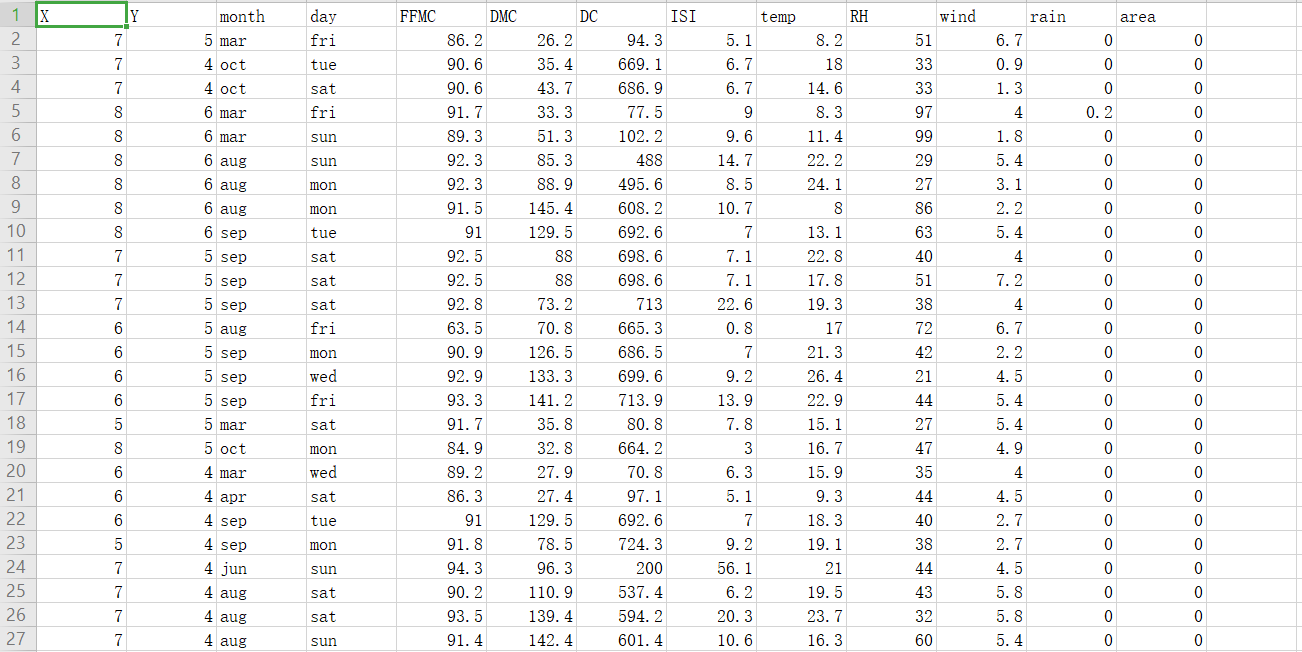
此次使用forestfires的数据集,共有12列特征
# 1. Montesinho公园地图内的X-x轴空间坐标:1到9
# 2. Montesinho公园地图内的 Y-y轴空间坐标:2到9
# 3.每年的月份-月:“ jan”到“ dec'
# 4.每天-星期几:从“周一”到“星期日”
# 5.FFMC
# - FWI系统中的FFMC指数:18.7至96.20 6. DMC-FWI系统中的DMC指数:1.1至291.3 7. DC- FWI系统的DC指数:7.9至860.6
# 8. ISI-FWI系统的ISI指数:0.0至56.10
# 9. temp- 摄氏温度:2.2至33.30
# 10. RH-相对湿度(%):15.0至100
# 11。风-以km / h为单位的风速:0.40至9.40
# 12.雨量-外部雨量,单位为mm / m2:0.0到6.4
# 13.面积-森林的燃烧面积(以ha为单位):0.00到1090.84
# (此输出变量非常偏向0.0,因此使用对数变换)
3. 引入要用的包
import csv
import copy
import calendar # 月份转换为数字的包
from math import log1p
from math import sqrt
from graphviz import Digraph
4.数据集的读取和处理
day为无关属性应该取出,area根据说明应该使用对数变换,month应该将字符转化为数字
def loadDataset(filename):
with open(filename, 'r') as f:
lines = csv.reader(f)
data_set = list(lines)
for i in range(len(data_set)):
del(data_set[i][0])
# 整理数据
for i in range(len(data_set)):
del(data_set[i][3])
category = data_set[0]
del(data_set[0])
for i in range(len(data_set)):
for j in range(len(data_set[0])):
if j == 2:
data_set[i][j] = str.capitalize(data_set[i][j])
data_set[i][j] = list(calendar.month_abbr).index(data_set[i][j])
data_set[i][j] = float(data_set[i][j])
if j == 11:
data_set[i][j] = log1p(data_set[i][j]+1)
return data_set, category
5.area与特征值分离
def split_data(data):
data_set = copy.deepcopy(data)
data_mat = []
label_mat = []
for i in range(len(data_set)):
label_mat.append(data_set[i][-1])
del(data_set[i][-1])
data_mat.append(data_set[i])
print(data_mat)
print(label_mat)
return data_mat, label_mat
6.误差计算
def split_data(data):
data_set = copy.deepcopy(data)
data_mat = []
label_mat = []
for i in range(len(data_set)):
label_mat.append(data_set[i][-1])
del(data_set[i][-1])
data_mat.append(data_set[i])
print(data_mat)
print(label_mat)
return data_mat, label_mat
7.划分节点的数据与特征的获取
def get_best_split_value(data, result):
data_set = set(data)
data_set = list(data_set)
data.sort()
length = len(data_set)
if length == 1:
return float("Inf"), float("Inf")
print(data_set)
split_value = []
for i in range(length-1):
split_value.append((data_set[i+1] + data_set[i])/2)
# if len(split_value) == 2:
# return (split_value[0]+split_value[1])/2, mse(data, (split_value[0]+split_value[1])/2, result)
m = []
for i in range(len(split_value)):
m.append(mse(data, split_value[i], result))
min_mse = 0
for i in range(len(m)):
if m[i] < m[min_mse]:
min_mse = i
print(m)
return split_value[min_mse], m[min_mse]
def get_best_feature(data, category):
length = len(category)-1
data_set, result = split_data(data)
feature_mse = []
split_feature_value = []
feature_values = []
for i in range(length):
feature_mse.append(0)
split_feature_value.append(0)
feature_values.append([])
for j in range(len(data_set)):
feature_values[i].append(data_set[j][i])
for i in range(length):
split_feature_value[i], feature_mse[i] = get_best_split_value(feature_values[i], result)
min_f = 0
for i in range(length):
if feature_mse[i] < feature_mse[min_f]:
min_f = i
print(feature_mse)
return min_f, split_feature_value[min_f]
8.树结点
class Node(object):
def __init__(self, category, item):
self.name = category
self.elem = item
self.lchild = None
self.rchild = None
9.叶子节点回归值的计算
def leaf_value(data):
sum = 0
for i in range(len(data)):
sum += data[i][-1]
return sum/len(data)
10.生成树
def creat_tree(data, labels, feature_labels=[]):
# 结束情况
if len(labels) == 1:
return Node('result', leaf_value(data))
if len(data) < 0.05*len(train_set):
return Node('result', leaf_value(data))
# 最优特征的标签
best_feature_num, best_feature_value = get_best_feature(data, labels)
feature_labels.append(labels[best_feature_num])
node = Node(labels[best_feature_num], best_feature_value)
ldata = []
rdata = []
for d in data:
if d[best_feature_num] <= best_feature_value:
del(d[best_feature_num])
ldata.append(d)
else:
del(d[best_feature_num])
rdata.append(d)
labels2 = copy.deepcopy(labels)
del(labels2[best_feature_num])
tree = node
tree.lchild = creat_tree(ldata, labels2, feature_labels)
tree.rchild = creat_tree(rdata, labels2, feature_labels)
return tree
11.树的遍历
def breadth_travel(tree):
"""广度遍历"""
queue = [tree]
while queue:
cur_node = queue.pop(0)
print(cur_node.name, end=" ")
print(cur_node.elem, end=" ")
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
print()
12.预测
def prediction(t_tree, test, labels):
result = []
test_mat, x = split_data(test)
for data in test_mat:
l = copy.deepcopy(labels)
tree = t_tree
for i in range(len(labels)):
if tree.name == "result":
result.append(tree.elem)
break
j = 0
while j:
if tree.name == l[j]:
break
j += 1
if data[j] <= tree.elem:
tree = tree.lchild
else:
tree = tree.rchild
del(l[j])
del(data[j])
return result
13.“链表”式树转化为字典树
def tree_to_dict(tree, tree_dict):
if tree.lchild == None and tree.rchild == None:
tree_dict[tree.name+str(tree.elem)] = str(tree.elem)
return tree_dict[tree.name+str(tree.elem)]
tree_dict[tree.name+str(tree.elem)] = {}
if tree.lchild != None:
tree_to_dict(tree.lchild, tree_dict[tree.name+str(tree.elem)])
if tree.rchild != None:
tree_to_dict(tree.rchild, tree_dict[tree.name+str(tree.elem)])
return tree_dict
14.树的可视化
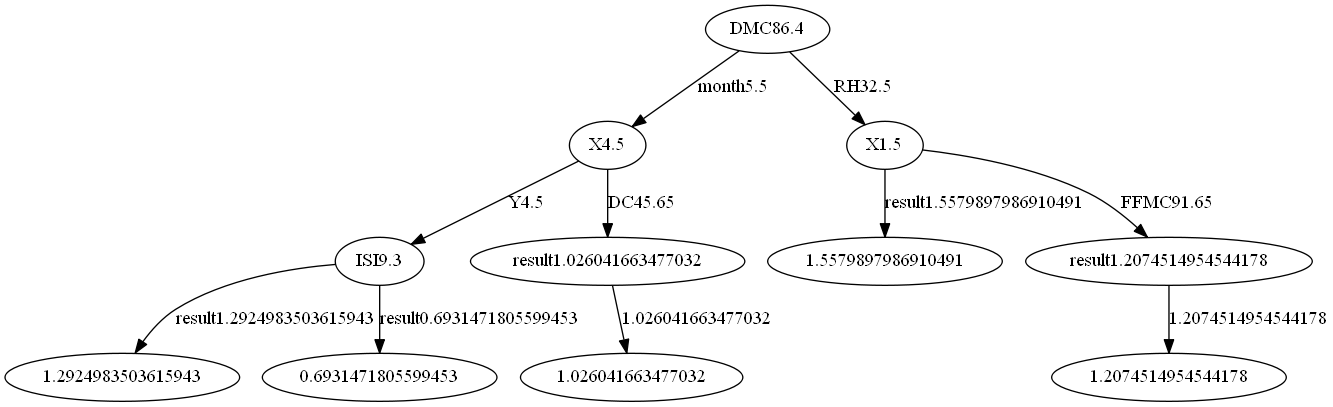
def plot_model(tree, name):
g = Digraph("G", filename=name, format='png', strict=False)
first_label = list(tree.keys())[0]
g.node("0", first_label)
_sub_plot(g, tree, "0")
g.view()
root = "0"
def _sub_plot(g, tree, inc):
global root
first_label = list(tree.keys())[0]
ts = tree[first_label]
if type(ts).__name__ != 'dict':
root = str(int(root) + 1)
g.node(root, str(tree[first_label]))
g.edge(inc, root, str(ts))
return
for i in ts.keys():
if isinstance(tree[first_label][i], dict):
root = str(int(root) + 1)
g.node(root, list(tree[first_label][i].keys())[0])
g.edge(inc, root, str(i))
_sub_plot(g, tree[first_label][i], root)
else:
root = str(int(root) + 1)
g.node(root, str(tree[first_label][i]))
g.edge(inc, root, str(i))
15.完整代码
import csv
import copy
import calendar
from math import log1p
from math import sqrt
from graphviz import Digraph
# 1. Montesinho公园地图内的X-x轴空间坐标:1到9
# 2. Montesinho公园地图内的 Y-y轴空间坐标:2到9
# 3.每年的月份-月:“ jan”到“ dec'
# 4.每天-星期几:从“周一”到“星期日”
# 5.FFMC
# - FWI系统中的FFMC指数:18.7至96.20 6. DMC-FWI系统中的DMC指数:1.1至291.3 7. DC- FWI系统的DC指数:7.9至860.6
# 8. ISI-FWI系统的ISI指数:0.0至56.10
# 9. temp- 摄氏温度:2.2至33.30
# 10. RH-相对湿度(%):15.0至100
# 11。风-以km / h为单位的风速:0.40至9.40
# 12.雨量-外部雨量,单位为mm / m2:0.0到6.4
# 13.面积-森林的燃烧面积(以ha为单位):0.00到1090.84
# (此输出变量非常偏向0.0,因此使用对数变换)
def loadDataset(filename):
with open(filename, 'r') as f:
lines = csv.reader(f)
data_set = list(lines)
for i in range(len(data_set)):
del(data_set[i][0])
# 整理数据
for i in range(len(data_set)):
del(data_set[i][3])
category = data_set[0]
del(data_set[0])
for i in range(len(data_set)):
for j in range(len(data_set[0])):
if j == 2:
data_set[i][j] = str.capitalize(data_set[i][j])
data_set[i][j] = list(calendar.month_abbr).index(data_set[i][j])
data_set[i][j] = float(data_set[i][j])
if j == 11:
data_set[i][j] = log1p(data_set[i][j]+1)
return data_set, category
def split_data(data):
data_set = copy.deepcopy(data)
data_mat = []
label_mat = []
for i in range(len(data_set)):
label_mat.append(data_set[i][-1])
del(data_set[i][-1])
data_mat.append(data_set[i])
print(data_mat)
print(label_mat)
return data_mat, label_mat
def mse(data_set, split_value, result):
left_num = 0
left_sum = 0
left_list = []
right_num = 0
right_sum = 0
rigth_list = []
for i in range(len(data_set)):
if data_set[i] <= split_value:
left_num += 1
left_sum += result[i]
left_list.append(result[i])
else:
right_num += 1
right_sum += result[i]
rigth_list.append(result[i])
c1 = left_sum/left_num
c2 = right_sum/right_num
m = 0
for i in range(len(left_list)):
m += pow((left_list[i]-c1), 2)
for i in range(len(rigth_list)):
m += pow((rigth_list[i]-c2), 2)
return m
def get_best_split_value(data, result):
data_set = set(data)
data_set = list(data_set)
data.sort()
length = len(data_set)
if length == 1:
return float("Inf"), float("Inf")
print(data_set)
split_value = []
for i in range(length-1):
split_value.append((data_set[i+1] + data_set[i])/2)
# if len(split_value) == 2:
# return (split_value[0]+split_value[1])/2, mse(data, (split_value[0]+split_value[1])/2, result)
m = []
for i in range(len(split_value)):
m.append(mse(data, split_value[i], result))
min_mse = 0
for i in range(len(m)):
if m[i] < m[min_mse]:
min_mse = i
print(m)
return split_value[min_mse], m[min_mse]
def get_best_feature(data, category):
length = len(category)-1
data_set, result = split_data(data)
feature_mse = []
split_feature_value = []
feature_values = []
for i in range(length):
feature_mse.append(0)
split_feature_value.append(0)
feature_values.append([])
for j in range(len(data_set)):
feature_values[i].append(data_set[j][i])
for i in range(length):
split_feature_value[i], feature_mse[i] = get_best_split_value(feature_values[i], result)
min_f = 0
for i in range(length):
if feature_mse[i] < feature_mse[min_f]:
min_f = i
print(feature_mse)
return min_f, split_feature_value[min_f]
class Node(object):
def __init__(self, category, item):
self.name = category
self.elem = item
self.lchild = None
self.rchild = None
def leaf_value(data):
sum = 0
for i in range(len(data)):
sum += data[i][-1]
return sum/len(data)
def creat_tree(data, labels, feature_labels=[]):
# 结束情况
if len(labels) == 1:
return Node('result', leaf_value(data))
if len(data) < 0.05*len(train_set):
return Node('result', leaf_value(data))
# 最优特征的标签
best_feature_num, best_feature_value = get_best_feature(data, labels)
feature_labels.append(labels[best_feature_num])
node = Node(labels[best_feature_num], best_feature_value)
ldata = []
rdata = []
for d in data:
if d[best_feature_num] <= best_feature_value:
del(d[best_feature_num])
ldata.append(d)
else:
del(d[best_feature_num])
rdata.append(d)
labels2 = copy.deepcopy(labels)
del(labels2[best_feature_num])
tree = node
tree.lchild = creat_tree(ldata, labels2, feature_labels)
tree.rchild = creat_tree(rdata, labels2, feature_labels)
return tree
def breadth_travel(tree):
"""广度遍历"""
queue = [tree]
while queue:
cur_node = queue.pop(0)
print(cur_node.name, end=" ")
print(cur_node.elem, end=" ")
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
print()
def prediction(t_tree, test, labels):
result = []
test_mat, x = split_data(test)
for data in test_mat:
l = copy.deepcopy(labels)
tree = t_tree
for i in range(len(labels)):
if tree.name == "result":
result.append(tree.elem)
break
j = 0
while j:
if tree.name == l[j]:
break
j += 1
if data[j] <= tree.elem:
tree = tree.lchild
else:
tree = tree.rchild
del(l[j])
del(data[j])
return result
def tree_to_dict(tree, tree_dict):
if tree.lchild == None and tree.rchild == None:
tree_dict[tree.name+str(tree.elem)] = str(tree.elem)
return tree_dict[tree.name+str(tree.elem)]
tree_dict[tree.name+str(tree.elem)] = {}
if tree.lchild != None:
tree_to_dict(tree.lchild, tree_dict[tree.name+str(tree.elem)])
if tree.rchild != None:
tree_to_dict(tree.rchild, tree_dict[tree.name+str(tree.elem)])
return tree_dict
def plot_model(tree, name):
g = Digraph("G", filename=name, format='png', strict=False)
first_label = list(tree.keys())[0]
g.node("0", first_label)
_sub_plot(g, tree, "0")
g.view()
root = "0"
def _sub_plot(g, tree, inc):
global root
first_label = list(tree.keys())[0]
ts = tree[first_label]
if type(ts).__name__ != 'dict':
root = str(int(root) + 1)
g.node(root, str(tree[first_label]))
g.edge(inc, root, str(ts))
return
for i in ts.keys():
if isinstance(tree[first_label][i], dict):
root = str(int(root) + 1)
g.node(root, list(tree[first_label][i].keys())[0])
g.edge(inc, root, str(i))
_sub_plot(g, tree[first_label][i], root)
else:
root = str(int(root) + 1)
g.node(root, str(tree[first_label][i]))
g.edge(inc, root, str(i))
if __name__ == "__main__":
test_set, category = loadDataset('forestfires_test.csv')
train_set, category = loadDataset('forestfires_train.csv')
print(category)
print(train_set)
print(test_set)
# a, b = get_best_feature(train_set, category)
# print(a)
# print(b)
my_tree = creat_tree(train_set, category)
breadth_travel(my_tree)
result = prediction(my_tree, test_set, category)
sme = 0
for i in range(len(result)):
sme += pow(abs(result[i]-test_set[i][-1]), 2)
print(sqrt(sme/len(result)))
tree_dict = {}
tree_dict = tree_to_dict(my_tree, tree_dict)
print(tree_dict)
plot_model(tree_dict, "forestfires.gv")
九、剪枝
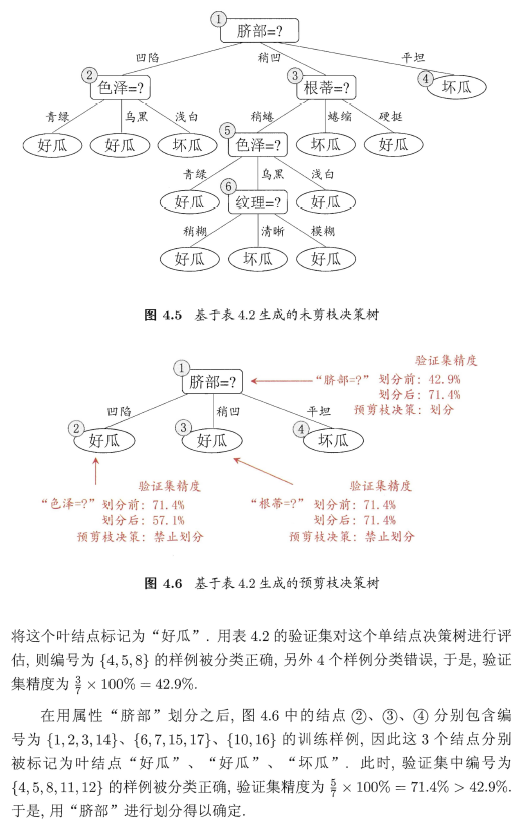
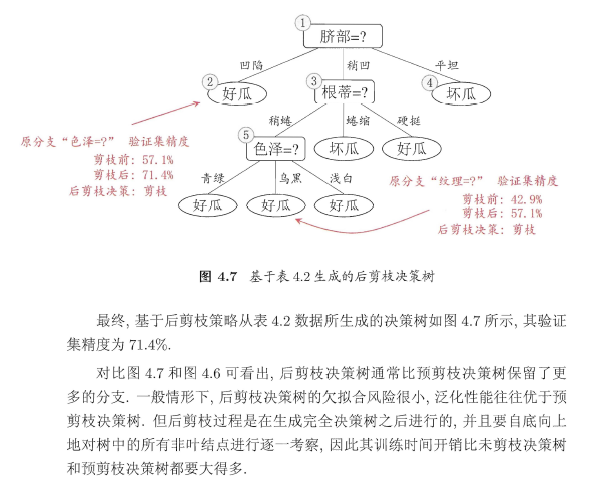
由于我自己写的后剪枝操作代码对于树没有任何修剪,这里就仅提供周志华《机器学习》中介绍的剪枝方法,不附带相关代码了。



from math import log
import operator
import pickle
def calcShannonEnt(dataSet):
# 统计数据数量
numEntries = len(dataSet)
# 存储每个label出现次数
label_counts = {}
# 统计label出现次数
for featVec in dataSet:
current_label = featVec[-1]
if current_label not in label_counts: # 提取label信息
label_counts[current_label] = 0 # 如果label未在dict中则加入
label_counts[current_label] += 1 # label计数
shannon_ent = 0 # 经验熵
# 计算经验熵
for key in label_counts:
prob = float(label_counts[key]) / numEntries
shannon_ent -= prob * log(prob, 2)
return shannon_ent
def splitDataSet(data_set, axis, value):
ret_dataset = []
for feat_vec in data_set:
if feat_vec[axis] == value:
reduced_feat_vec = feat_vec[:axis]
reduced_feat_vec.extend(feat_vec[axis + 1:])
ret_dataset.append(reduced_feat_vec)
return ret_dataset
def chooseBestFeatureToSplit(dataSet):
# 特征数量
num_features = len(dataSet[0]) - 1
# 计算数据香农熵
base_entropy = calcShannonEnt(dataSet)
# 信息增益
best_info_gain = 0.0
# 最优特征索引值
best_feature = -1
# 遍历所有特征
for i in range(num_features):
# 获取dataset第i个特征
feat_list = [exampel[i] for exampel in dataSet]
# 创建set集合,元素不可重合
unique_val = set(feat_list)
# 经验条件熵
new_entropy = 0.0
# 计算信息增益
for value in unique_val:
# sub_dataset划分后的子集
sub_dataset = splitDataSet(dataSet, i, value)
# 计算子集的概率
prob = len(sub_dataset) / float(len(dataSet))
# 计算经验条件熵
new_entropy += prob * calcShannonEnt(sub_dataset)
# 信息增益
info_gain = base_entropy - new_entropy
# 打印每个特征的信息增益
print("第%d个特征的信息增益为%.3f" % (i, info_gain))
# 计算信息增益
if info_gain > best_info_gain:
# 更新信息增益
best_info_gain = info_gain
# 记录信息增益最大的特征的索引值
best_feature = i
print("最优索引值:" + str(best_feature))
print()
return best_feature
def majority_cnt(class_list):
class_count = {}
# 统计class_list中每个元素出现的次数
for vote in class_list:
if vote not in class_count:
class_count[vote] = 0
class_count[vote] += 1
# 根据字典的值降序排列
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0]
def creat_tree(dataSet, labels, featLabels):
# 取分类标签(是否放贷:yes or no)
class_list = [exampel[-1] for exampel in dataSet]
# 如果类别完全相同则停止分类
if class_list.count(class_list[0]) == len(class_list):
return class_list[0]
# 遍历完所有特征时返回出现次数最多的类标签
if len(dataSet[0]) == 1:
return majority_cnt(class_list)
# 选择最优特征
best_feature = chooseBestFeatureToSplit(dataSet)
# 最优特征的标签
best_feature_label = labels[best_feature]
featLabels.append(best_feature_label)
# 根据最优特征的标签生成树
my_tree = {best_feature_label: {}}
# 删除已使用标签
del(labels[best_feature])
# 得到训练集中所有最优特征的属性值
feat_value = [exampel[best_feature] for exampel in dataSet]
# 去掉重复属性值
unique_vls = set(feat_value)
for value in unique_vls:
my_tree[best_feature_label][value] = creat_tree(splitDataSet(dataSet, best_feature, value), labels, featLabels)
return my_tree
def get_num_leaves(my_tree):
num_leaves = 0
first_str = next(iter(my_tree))
second_dict = my_tree[first_str]
for key in second_dict.keys():
if type(second_dict[key]).__name__ == 'dict':
num_leaves += get_num_leaves(second_dict[key])
else:
num_leaves += 1
return num_leaves
def get_tree_depth(my_tree):
max_depth = 0 # 初始化决策树深度
firsr_str = next(iter(my_tree)) # python3中myTree.keys()返回的是dict_keys,不在是list,所以不能使用myTree.keys()[0]的方法获取结点属性,可以使用list(myTree.keys())[0]
second_dict = my_tree[firsr_str] # 获取下一个字典
for key in second_dict.keys():
if type(second_dict[key]).__name__ == 'dict': # 测试该结点是否为字典,如果不是字典,代表此结点为叶子结点
this_depth = 1 + get_tree_depth(second_dict[key])
else:
this_depth = 1
if this_depth > max_depth:
max_depth = this_depth # 更新层数
return max_depth
def classify(input_tree, feat_labels, test_vec):
# 获取决策树节点
first_str = next(iter(input_tree))
# 下一个字典
second_dict = input_tree[first_str]
feat_index = feat_labels.index(first_str)
for key in second_dict.keys():
if test_vec[feat_index] == key:
if type(second_dict[key]).__name__ == 'dict':
class_label = classify(second_dict[key], feat_labels, test_vec)
else:
class_label = second_dict[key]
return class_label
def storeTree(input_tree, filename):
# 存储树
with open(filename, 'wb') as fw:
pickle.dump(input_tree, fw)
def grabTree(filename):
# 读取树
fr = open(filename, 'rb')
return pickle.load(fr)
if __name__ == "__main__":
# 数据集
dataSet = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
# [1, 0, 0, 0, 'yes'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
# 分类属性
labels = ['年龄', '有工作', '有自己的房子', '信贷情况']
print(dataSet)
print()
print(calcShannonEnt(dataSet))
print()
featLabels = []
myTree = creat_tree(dataSet, labels, featLabels)
print(myTree)
print(get_tree_depth(myTree))
print(get_num_leaves(myTree))
#测试数据
testVec = [0, 1, 1, 1]
result = classify(myTree, featLabels, testVec)
if result == 'yes':
print('放贷')
if result == 'no':
print('不放贷')
# 存储树
storeTree(myTree,'classifierStorage.txt')
# 读取树
myTree2 = grabTree('classifierStorage.txt')
print(myTree2)
testVec2 = [1, 0]
result2 = classify(myTree2, featLabels, testVec)
if result2 == 'yes':
print('放贷')
if result2 == 'no':
print('不放贷')
# 输出结果如下:
[[0, 0, 0, 0, 'no'], [0, 0, 0, 1, 'no'], [0, 1, 0, 1, 'yes'], [0, 1, 1, 0, 'yes'], [0, 0, 0, 0, 'no'], [1, 0, 0, 0, 'no'], [1, 0, 0, 1, 'no'], [1, 1, 1, 1, 'yes'], [1, 0, 1, 2, 'yes'], [1, 0, 1, 2, 'yes'], [2, 0, 1, 2, 'yes'], [2, 0, 1, 1, 'yes'], [2, 1, 0, 1, 'yes'], [2, 1, 0, 2, 'yes'], [2, 0, 0, 0, 'no']]
0.9709505944546686
第0个特征的信息增益为0.083
第1个特征的信息增益为0.324
第2个特征的信息增益为0.420
第3个特征的信息增益为0.363
最优索引值:2
第0个特征的信息增益为0.252
第1个特征的信息增益为0.918
第2个特征的信息增益为0.474
最优索引值:1
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
2
3
放贷
{'有自己的房子': {0: {'有工作': {0: 'no', 1: 'yes'}}, 1: 'yes'}}
放贷
import csv
import operator
import copy
import numpy as np
# 0PassengerId:乘客的ID 不重要
# 1Survived:乘客是否获救,Key:0=没获救,1=已获救
# 2Pclass:乘客船舱等级(1/2/3三个等级舱位)
# 3Name:乘客姓名 不重要
# 4Sex:性别
# 5Age:年龄
# 6SibSp:乘客在船上的兄弟姐妹/配偶数量
# 7Parch:乘客在船上的父母/孩子数量
# 8Ticket:船票号 不重要
# 9Fare:船票价
# 10Cabin:客舱号码 不重要
# 11Embarked:登船的港口 不重要
def loadDataset(filename):
with open(filename, 'r') as f:
lines = csv.reader(f)
data_set = list(lines)
if filename != 'titanic.csv':
for i in range(len(data_set)):
del(data_set[i][0])
# 整理数据
for i in range(len(data_set)):
del(data_set[i][0])
del(data_set[i][2])
data_set[i][4] += data_set[i][5]
del(data_set[i][5])
del(data_set[i][5])
del(data_set[i][6])
del(data_set[i][-1])
category = data_set[0]
del (data_set[0])
# 转换数据格式
for data in data_set:
data[0] = int(data[0])
data[1] = int(data[1])
if data[3] != '':
data[3] = float(data[3])
else:
data[3] = None
data[4] = float(data[4])
data[5] = float(data[5])
# 补全缺失值 转换记录方式 分类
for data in data_set:
if data[3] is None:
data[3] = 28
# male : 1, female : 0
if data[2] == 'male':
data[2] = 1
else:
data[2] = 0
# age <25 为0, 25<=age<31为1,age>=31为2
if data[3] < 60: # 但是测试得60分界准确率最高???!!!
data[3] = 0
else:
data[3] = 1
# sibsp&parcg以2为界限,小于为0,大于为1
if data[4] < 2:
data[4] = 0
else:
data[4] = 1
# fare以64为界限
if data[-1] < 64:
data[-1] = 0
else:
data[-1] = 1
return data_set, category
def gini(data, i):
num = len(data)
label_counts = [0, 0, 0, 0]
p_count = [0, 0, 0, 0]
gini_count = [0, 0, 0, 0]
for d in data:
label_counts[d[i]] += 1
for l in range(len(label_counts)):
for d in data:
if label_counts[l] != 0 and d[0] == 1 and d[i] == l:
p_count[l] += 1
print(label_counts)
print(p_count)
for l in range(len(label_counts)):
if label_counts[l] != 0:
gini_count[l] = 2*(p_count[l]/label_counts[l])*(1 - p_count[l]/label_counts[l])
gini_p = 0
for l in range(len(gini_count)):
gini_p += (label_counts[l]/num)*gini_count[l]
print(gini_p)
return gini_p
def get_best_feature(data, category):
if len(category) == 2:
return 1, category[1]
feature_num = len(category) - 1
data_num = len(data)
feature_gini = []
for i in range(1, feature_num+1):
feature_gini.append(gini(data, i))
min = 0
for i in range(len(feature_gini)):
if feature_gini[i] < feature_gini[min]:
min = i
print(feature_gini)
print(category)
print(min+1)
print(category[min+1])
return min+1, category[min + 1]
def majority_cnt(class_list):
class_count = {}
# 统计class_list中每个元素出现的次数
for vote in class_list:
if vote not in class_count:
class_count[vote] = 0
class_count[vote] += 1
# 根据字典的值降序排列
sorted_class_count = sorted(class_count.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count[0][0]
class Node(object):
def __init__(self, item):
self.name = item
self.lchild = None
self.rchild = None
def creat_tree(data, labels, feature_labels=[]):
# 三种结束情况
# 取分类标签(survivor or death)
class_list = [exampel[0] for exampel in data]
if class_list == []:
return Node(0)
# 如果类别完全相同则停止分类
if class_list.count(class_list[0]) == len(class_list):
return Node(class_list[0])
# 遍历完所有特征时返回出现次数最多的类标签
if len(data[0]) == 1:
return Node(majority_cnt(class_list))
# 最优特征的标签
best_feature_num, best_feature_label = get_best_feature(data, labels)
feature_labels.append(best_feature_label)
node = Node(best_feature_label)
ldata = []
rdata = []
for d in data:
if d[best_feature_num] == 1:
del(d[best_feature_num])
ldata.append(d)
else:
del(d[best_feature_num])
rdata.append(d)
labels2 = copy.deepcopy(labels)
del(labels2[best_feature_num])
tree = node
tree.lchild = creat_tree(ldata, labels2, feature_labels)
tree.rchild = creat_tree(rdata, labels2, feature_labels)
return tree
def breadth_travel(tree):
"""广度遍历"""
queue = [tree]
while queue:
cur_node = queue.pop(0)
print(cur_node.name, end=" ")
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
print()
def prediction(t_tree, test, labels):
result = []
for data in test:
l = copy.deepcopy(labels)
tree = t_tree
for i in range(len(labels)):
if tree.name == 1 or tree.name == 0:
result.append(tree.name)
break
if len(data) == 1:
result.append(0)
break
j = 1
while j < len(data)-1:
if tree.name == l[j]:
break
j += 1
if data[j] == 1:
tree = tree.lchild
else:
tree = tree.rchild
del(l[j])
del(data[j])
return result
if __name__ == "__main__":
test_set, category = loadDataset('data/data43004/titanic_test.csv')
train_set, category = loadDataset('data/data43004/titanic_train.csv')
print(category)
print(train_set)
print()
print(test_set)
my_tree = creat_tree(train_set, category)
print(my_tree)
breadth_travel(my_tree)
print(category)
print(test_set)
test = copy.deepcopy(test_set)
result = prediction(my_tree, test_set, category)
print(len(test_set))
print(result)
counts = 0
for i in range(len(test_set)):
if test_set[i][0] == result[i]:
counts += 1
print(counts)
accurancy = counts/len(test_set)
print(accurancy)
import csv
import copy
import calendar
from math import log1p
from math import sqrt
from graphviz import Digraph
# 1. Montesinho公园地图内的X-x轴空间坐标:1到9
# 2. Montesinho公园地图内的 Y-y轴空间坐标:2到9
# 3.每年的月份-月:“ jan”到“ dec'
# 4.每天-星期几:从“周一”到“星期日”
# 5.FFMC
# - FWI系统中的FFMC指数:18.7至96.20 6. DMC-FWI系统中的DMC指数:1.1至291.3 7. DC- FWI系统的DC指数:7.9至860.6
# 8. ISI-FWI系统的ISI指数:0.0至56.10
# 9. temp- 摄氏温度:2.2至33.30
# 10. RH-相对湿度(%):15.0至100
# 11。风-以km / h为单位的风速:0.40至9.40
# 12.雨量-外部雨量,单位为mm / m2:0.0到6.4
# 13.面积-森林的燃烧面积(以ha为单位):0.00到1090.84
# (此输出变量非常偏向0.0,因此使用对数变换)
def loadDataset(filename):
with open(filename, 'r') as f:
lines = csv.reader(f)
data_set = list(lines)
for i in range(len(data_set)):
del(data_set[i][0])
# 整理数据
for i in range(len(data_set)):
del(data_set[i][3])
category = data_set[0]
del(data_set[0])
for i in range(len(data_set)):
for j in range(len(data_set[0])):
if j == 2:
data_set[i][j] = str.capitalize(data_set[i][j])
data_set[i][j] = list(calendar.month_abbr).index(data_set[i][j])
data_set[i][j] = float(data_set[i][j])
if j == 11:
data_set[i][j] = log1p(data_set[i][j]+1)
return data_set, category
def split_data(data):
data_set = copy.deepcopy(data)
data_mat = []
label_mat = []
for i in range(len(data_set)):
label_mat.append(data_set[i][-1])
del(data_set[i][-1])
data_mat.append(data_set[i])
print(data_mat)
print(label_mat)
return data_mat, label_mat
def mse(data_set, split_value, result):
left_num = 0
left_sum = 0
left_list = []
right_num = 0
right_sum = 0
rigth_list = []
for i in range(len(data_set)):
if data_set[i] <= split_value:
left_num += 1
left_sum += result[i]
left_list.append(result[i])
else:
right_num += 1
right_sum += result[i]
rigth_list.append(result[i])
c1 = left_sum/left_num
c2 = right_sum/right_num
m = 0
for i in range(len(left_list)):
m += pow((left_list[i]-c1), 2)
for i in range(len(rigth_list)):
m += pow((rigth_list[i]-c2), 2)
return m
def get_best_split_value(data, result):
data_set = set(data)
data_set = list(data_set)
data.sort()
length = len(data_set)
if length == 1:
return float("Inf"), float("Inf")
print(data_set)
split_value = []
for i in range(length-1):
split_value.append((data_set[i+1] + data_set[i])/2)
# if len(split_value) == 2:
# return (split_value[0]+split_value[1])/2, mse(data, (split_value[0]+split_value[1])/2, result)
m = []
for i in range(len(split_value)):
m.append(mse(data, split_value[i], result))
min_mse = 0
for i in range(len(m)):
if m[i] < m[min_mse]:
min_mse = i
print(m)
return split_value[min_mse], m[min_mse]
def get_best_feature(data, category):
length = len(category)-1
data_set, result = split_data(data)
feature_mse = []
split_feature_value = []
feature_values = []
for i in range(length):
feature_mse.append(0)
split_feature_value.append(0)
feature_values.append([])
for j in range(len(data_set)):
feature_values[i].append(data_set[j][i])
for i in range(length):
split_feature_value[i], feature_mse[i] = get_best_split_value(feature_values[i], result)
min_f = 0
for i in range(length):
if feature_mse[i] < feature_mse[min_f]:
min_f = i
print(feature_mse)
return min_f, split_feature_value[min_f]
class Node(object):
def __init__(self, category, item):
self.name = category
self.elem = item
self.lchild = None
self.rchild = None
def leaf_value(data):
sum = 0
for i in range(len(data)):
sum += data[i][-1]
return sum/len(data)
def creat_tree(data, labels, feature_labels=[]):
# 结束情况
if len(labels) == 1:
return Node('result', leaf_value(data))
if len(data) < 0.05*len(train_set):
return Node('result', leaf_value(data))
# 最优特征的标签
best_feature_num, best_feature_value = get_best_feature(data, labels)
feature_labels.append(labels[best_feature_num])
node = Node(labels[best_feature_num], best_feature_value)
ldata = []
rdata = []
for d in data:
if d[best_feature_num] <= best_feature_value:
del(d[best_feature_num])
ldata.append(d)
else:
del(d[best_feature_num])
rdata.append(d)
labels2 = copy.deepcopy(labels)
del(labels2[best_feature_num])
tree = node
tree.lchild = creat_tree(ldata, labels2, feature_labels)
tree.rchild = creat_tree(rdata, labels2, feature_labels)
return tree
def breadth_travel(tree):
"""广度遍历"""
queue = [tree]
while queue:
cur_node = queue.pop(0)
print(cur_node.name, end=" ")
print(cur_node.elem, end=" ")
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
print()
def prediction(t_tree, test, labels):
result = []
test_mat, x = split_data(test)
for data in test_mat:
l = copy.deepcopy(labels)
tree = t_tree
for i in range(len(labels)):
if tree.name == "result":
result.append(tree.elem)
break
j = 0
while j:
if tree.name == l[j]:
break
j += 1
if data[j] <= tree.elem:
tree = tree.lchild
else:
tree = tree.rchild
del(l[j])
del(data[j])
return result
def tree_to_dict(tree, tree_dict):
if tree.lchild == None and tree.rchild == None:
tree_dict[tree.name+str(tree.elem)] = str(tree.elem)
return tree_dict[tree.name+str(tree.elem)]
tree_dict[tree.name+str(tree.elem)] = {}
if tree.lchild != None:
tree_to_dict(tree.lchild, tree_dict[tree.name+str(tree.elem)])
if tree.rchild != None:
tree_to_dict(tree.rchild, tree_dict[tree.name+str(tree.elem)])
return tree_dict
def plot_model(tree, name):
g = Digraph("G", filename=name, format='png', strict=False)
first_label = list(tree.keys())[0]
g.node("0", first_label)
_sub_plot(g, tree, "0")
g.view()
root = "0"
def _sub_plot(g, tree, inc):
global root
first_label = list(tree.keys())[0]
ts = tree[first_label]
if type(ts).__name__ != 'dict':
root = str(int(root) + 1)
g.node(root, str(tree[first_label]))
g.edge(inc, root, str(ts))
return
for i in ts.keys():
if isinstance(tree[first_label][i], dict):
root = str(int(root) + 1)
g.node(root, list(tree[first_label][i].keys())[0])
g.edge(inc, root, str(i))
_sub_plot(g, tree[first_label][i], root)
else:
root = str(int(root) + 1)
g.node(root, str(tree[first_label][i]))
g.edge(inc, root, str(i))
if __name__ == "__main__":
test_set, category = loadDataset('data/data43017/test.csv')
train_set, category = loadDataset('data/data43017/train.csv')
print(category)
print(train_set)
print(test_set)
# a, b = get_best_feature(train_set, category)
# print(a)
# print(b)
my_tree = creat_tree(train_set, category)
breadth_travel(my_tree)
result = prediction(my_tree, test_set, category)
sme = 0
for i in range(len(result)):
sme += pow(abs(result[i]-test_set[i][-1]), 2)
print(sqrt(sme/len(result)))
tree_dict = {}
tree_dict = tree_to_dict(my_tree, tree_dict)
print(tree_dict)
plot_model(tree_dict, "forestfires.gv")
