形式语言总结
形式语言马上考试了,每天写一点笔记复习一下,更新中ing
第一章DFA
DFA是一种特殊的NFA,
第2章NFA
1.设计一个由01构成的串,1是偶数0是奇数的NFA
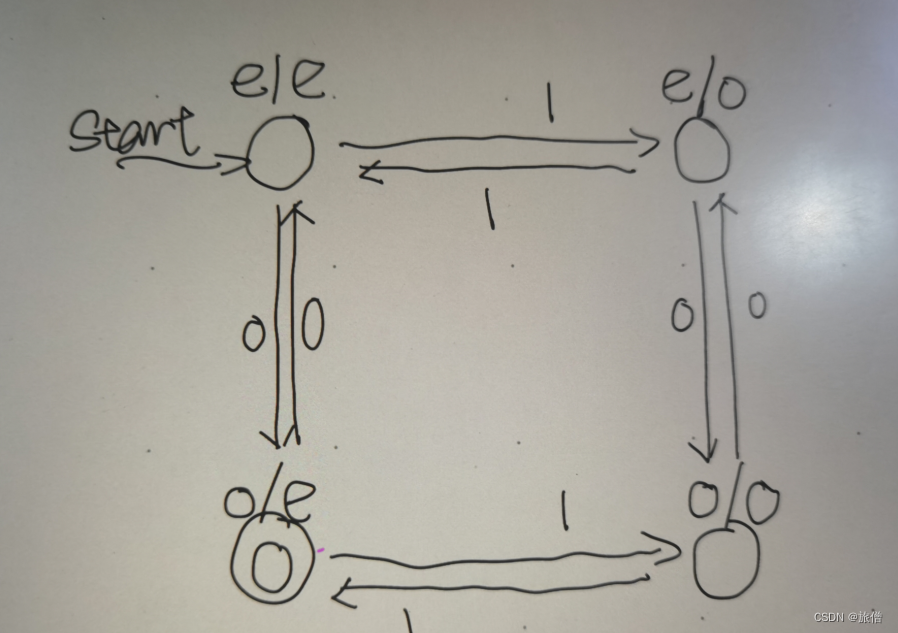
对0 1的状态进行区分
2.对以下几种语言设计NFA :

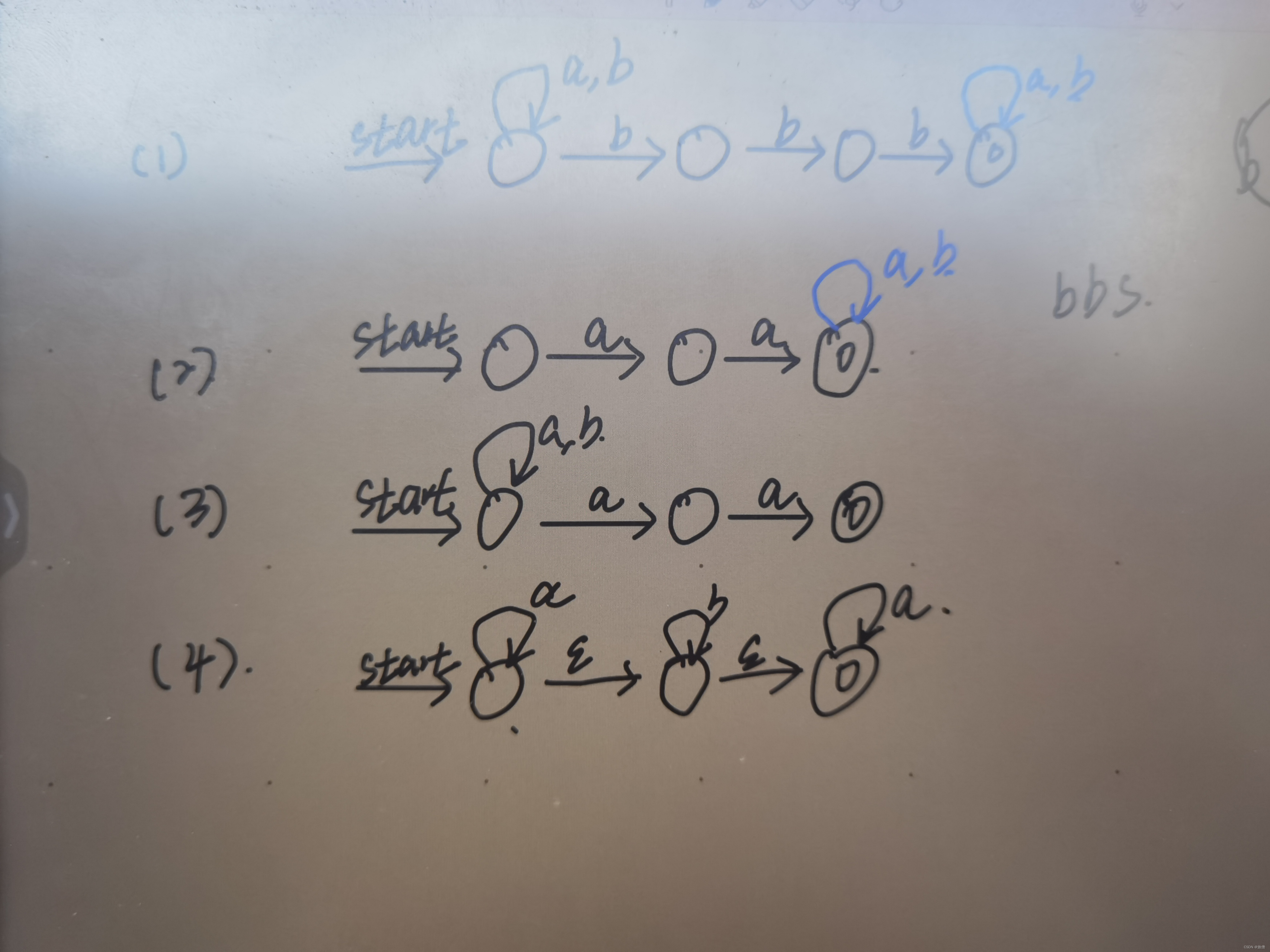
第3-4章正则表达式
正则表达式的设计举例
正则表达式的运算

正则表达式的优先级

举例
1.倒数第三个字符是1
(0+1)*1(0+1)(0+1)
2.不含有连续的0
(1+01)*(0+)
3.含有000
(0+1)*000(0+1)*
4.不含000/111的正则语言(/代表两个式等价的)
(1+01+001)*(+0+00) / 1*(0
+00
)
DFA 正则表达式
正则表达式
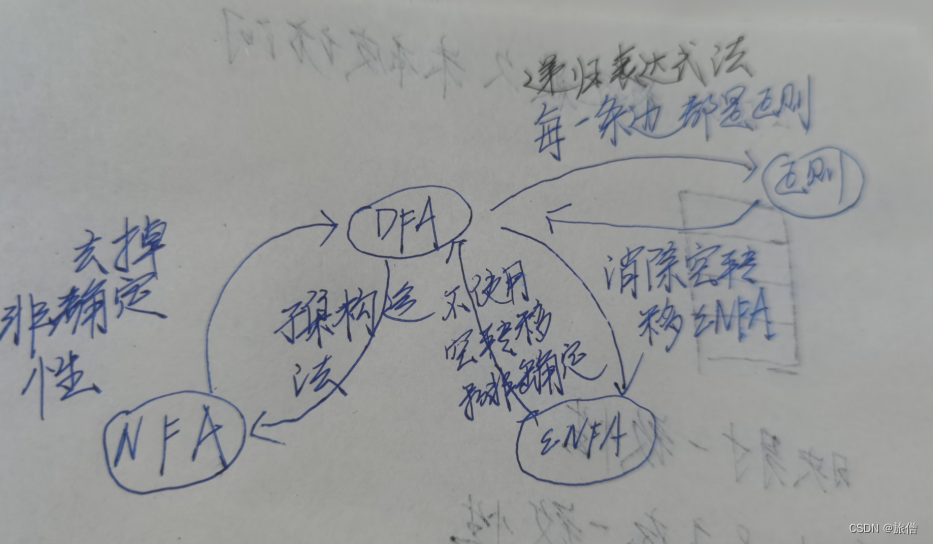
为什么要引入:有的时候我们做设计正则表达式习题的时候发现直接想很困难,我们不如利用正则表达式和DFA之间的等价性,构造出DFA,进而构造正则表达式。
1.设计不含001/110的正则表达式
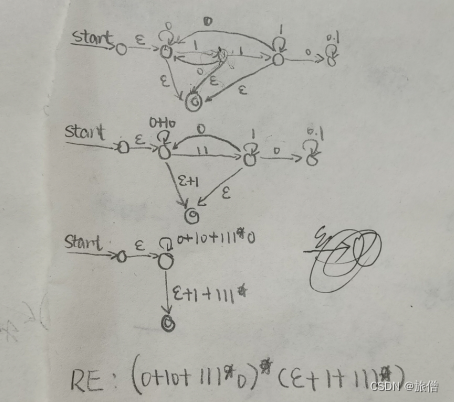
2.设计不含010/101的正则表达式
方法1:直接猜测法:
方法2:DFA转正则表达式

3.设计不含001/110的正则语言

4 . L = { w∈{0,1}* | w contains both 01 and 10 as substrings }
这个题的出错点在于可能忘记考虑010 101的情况
分类相加的方法:
直接的方法 :合并情况的方法
5.The set of all strings with an equal number of 0's and 1's, such that no prefix has two more 0's than 1's, nor two more 1's than 0's.
6. Let L={ w | w∈{0,1}* and if there are two 0s of w, they must be separated by 1 or 11 }
|11 | 11 |
explaination : | 10 | 10 |................................
正则语言的性质
泵引理老师上课也讲了 不少,感觉上课再看看书上的例题熟悉一下思路基本就没问题了,后面PDA那里也有一个泵引理,不过考试还是喜欢正则语言的泵引理。我自己的感觉是取语言中的一个串,如果不符合那么这个语言就不是正则语言。
1.证明泵引理
- 往多泵
- 往少泵
- 利用语言的封闭性证明:if
都是正则语言L =
,或者其反转
也是正则语言,如果不是正则语言那么L不一定不是正则语言。
具体实例见第四章习题,一般的方法是取语言中的子串。利用语言中的一个元素不是正则来确定不是正则语言。

1.证明回文字符不是正则语言:

2.DFA的最小化:
第5章上下文无关文法:
设计文法:
做题的时候发现了一个正则表达式到文法的算法 R规则
根据正则式推导右线性文法_右线性文法表达ab*_Pluto °的博客-CSDN博客
举例
设计文法的关键在于理解递归性,文法是一个迭代器
1.The set {| i ≠ j or j ≠ k}, that is, the set of strings of a's followed by b's followed by c's, such that there are either a different number of a's and b's or a different number of b's and c's, or both.

上方的做法是错误的做法 因为没有考虑i=j=k的情况。
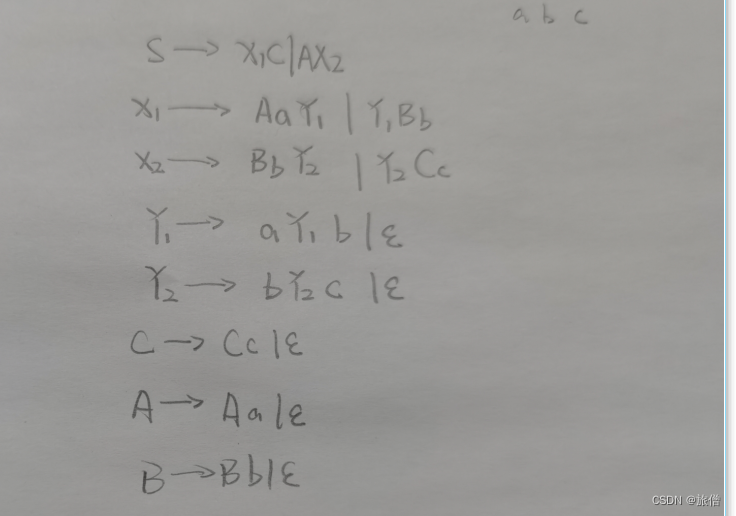
修改之后的结果
2.The set {|i=j|j=k} is generated by G = ( { S , T , U , A , C } , { a , b , c } , P , S )) with production P:
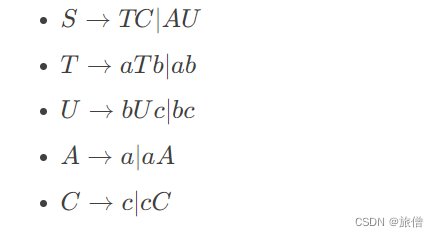
3.请为语言L = {}设计文法

4.设计0、1构成的串的文法,0 1数量不相等.
5. The set of all strings 0’s and 1’s that are not of the form ww, that is , not equal to any string repeated.
6.The set of all strings with twice as many 0's as 1's.
7.设计 Lj≥2i = {| j ≥ 2i} 的文法.
- S→AB
- A→aAbb I 空串
- B→Bb I 空串
8. L= { | n
0 and n
3}
9.L(0 0* 11* 22* 00* 11* 22* 00* 11* 22*) Hint : The language defined by the regular expression.
分析:看起来像是012202012然后每一个的子字符可以重复,
相当于三次方
10. L = { |}
explaination:分成两种情况:

11.L ={ }
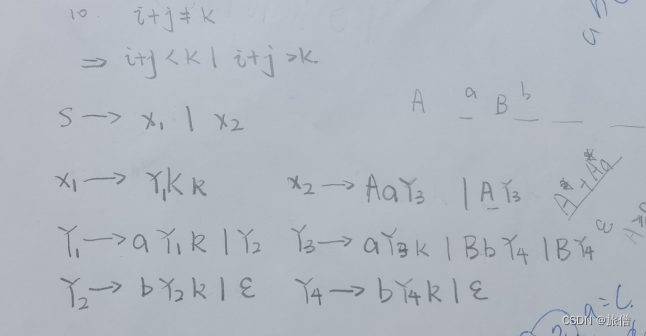
验证某个串是否在文法中:派生 使用树来判断字符串是否在文法中
12.构造右线性文法:
 (1)
(1)
(2)
(3)
(4) 正则语言是(a+b)*(aa+bb)*(a+b)* 所以根据R规则
13. Design CFG for strings in {0,1} * in which the number of 0s is greater than or equal to the number of 1s.
14.Design CFG for L = {w ∈ {(, )} ∗ | w is a string of balanced parentheses}.(括号匹配)
文法的歧义性
1.判断一个语言具有歧义性,画出两种树

2.让你消除歧义性:重新设计文法。
文法的化简

第6章下推自动机
下推自动机相当于 栈:他既有非确定性也支持空转移,他拥有栈的性质,体现在它能够识别w
但是不能识别ww和
(图灵机可以识别)语言。
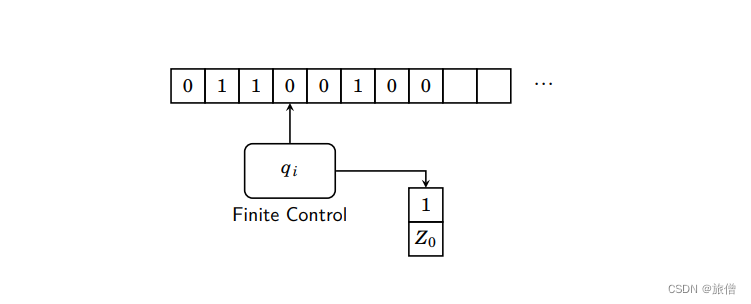
将000入栈,每读入一个1弹出一个0....当输入完所有的1栈空,则就是识别0n1n的PDA
每次根据读头、状态、栈顶三个东西进行跳转,修改当前状态、改变读头,弹出一个符号往栈里压入多个符号 多个符号构成的字符串的长度可以是0个1个或者多个,0个代表弹出栈顶元素,1个代表保持或者修改栈顶符号,多个表示弹出一个符号压入多个符号。
PDA的设计
一般有两种方式:空栈接受和终态接受,他们是等价的,空栈接受有利于消除一些无用的状态。
构造PDA关键在于理解非确定性。
1.设计识别{|n
1}的PDA
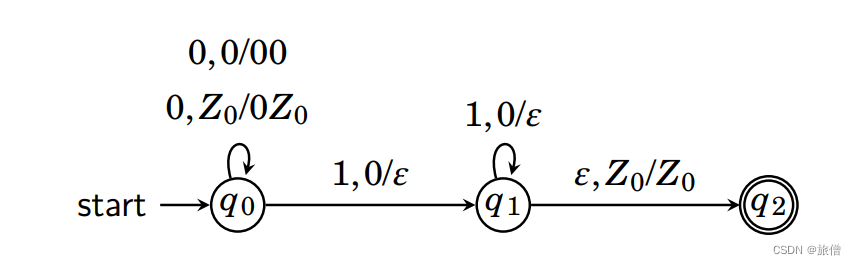
2.升级版设计识别{|n
0}的PDA
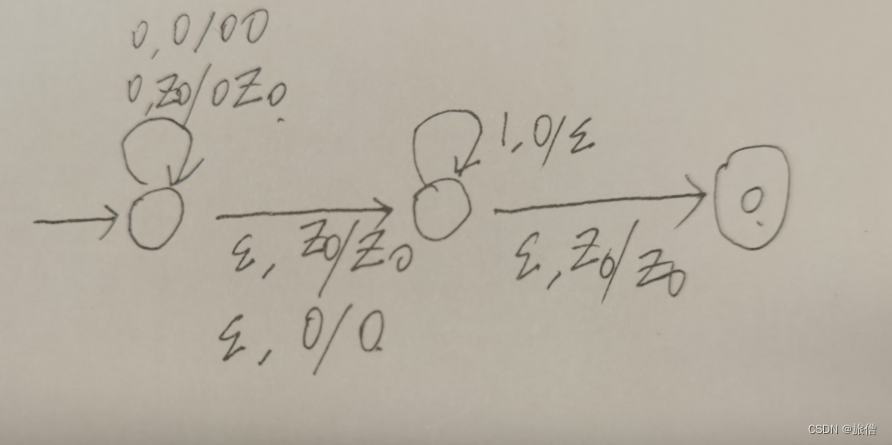
*思考:1当识别0001111扫描完整个串的空串才能停下来在q3接受状态如果后边还有字符他会卡死Z0可以判断是否扫描完整个串.2.000111我00之间也可以通过空转移到达q2但是此时读头上是0,而我只能接受1的读字符串的动作因此会卡死,由于PDA具有非确定性,只有在wwr的形式上才能接受,否则就会卡死。
3.设计识别{w|w
}的PDA
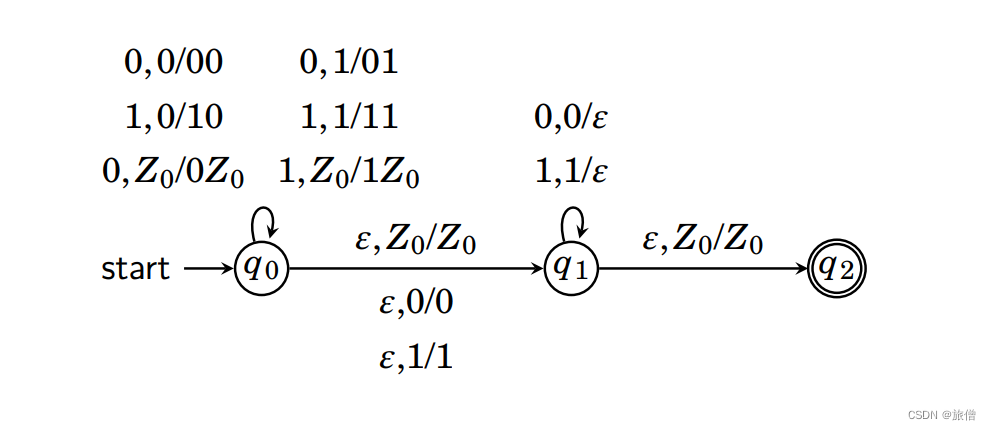
4.The set of all strings of 0’s and l’s such that no prefix has more l’s than 0’s.
5.接受 Leq = {w ∈ {0,1} | w 中字符 0 和 1 的数量相同 } 的 PDA
以空栈方式接受
![]()
思路,如果第一个读入1/0第二个读入0/1那么直接弹栈,如果都是0或者都是1,那么压栈,直到栈弹空。
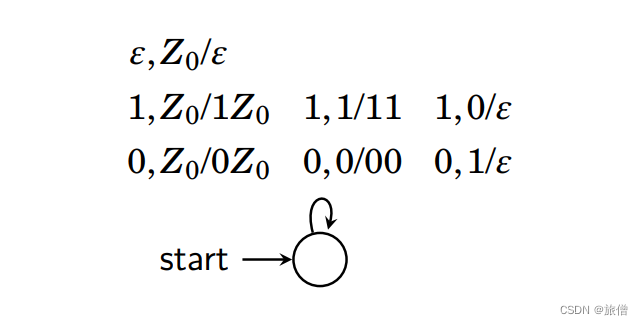
以终态方式接受:
6.接受 L = {| 0 ≤ n ≤ m ≤ 2n } 的 PDA
方法1:由于PDA具有非确定性,所以可以让一次弹入1个或者2个0,最后读入1再弹出1

方法2:第一次读入n个0,第二次添加情况读入1弹出一个0或者两个0
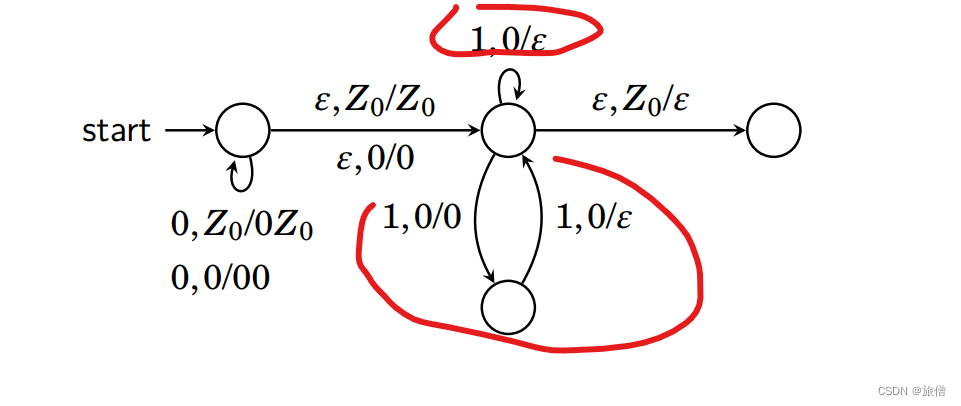
思考:如果我们设计这种语言对应的文法:
左边保证了他小于2n,右边保证了他大于n,而“|”体现了文法的非确定性。
7.
![]()
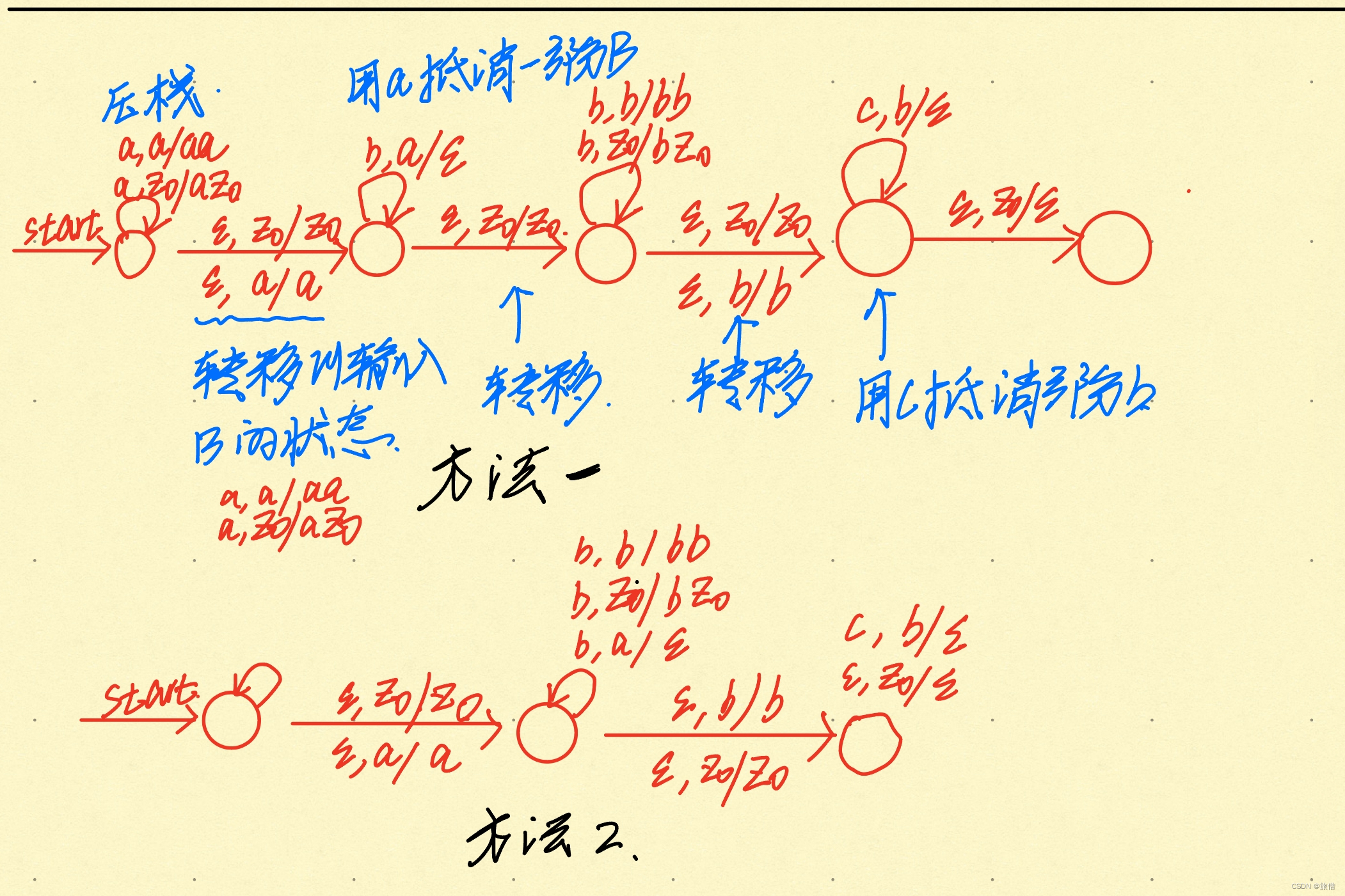
PDA性质
由于PDA具有非确定性,仅用状态无法很好描述当前的性质


终态方式和空栈方式接受PDA


等价性的证明(不考但是对理解PDA有用)

用构造
用在PF上增加一个新状态,并且利用空转移,将pn的栈底X0压入栈中,pf模拟pn该接受的字符串

PDA和CFG的转换
由于PDA的非确定性,他有很多种形式
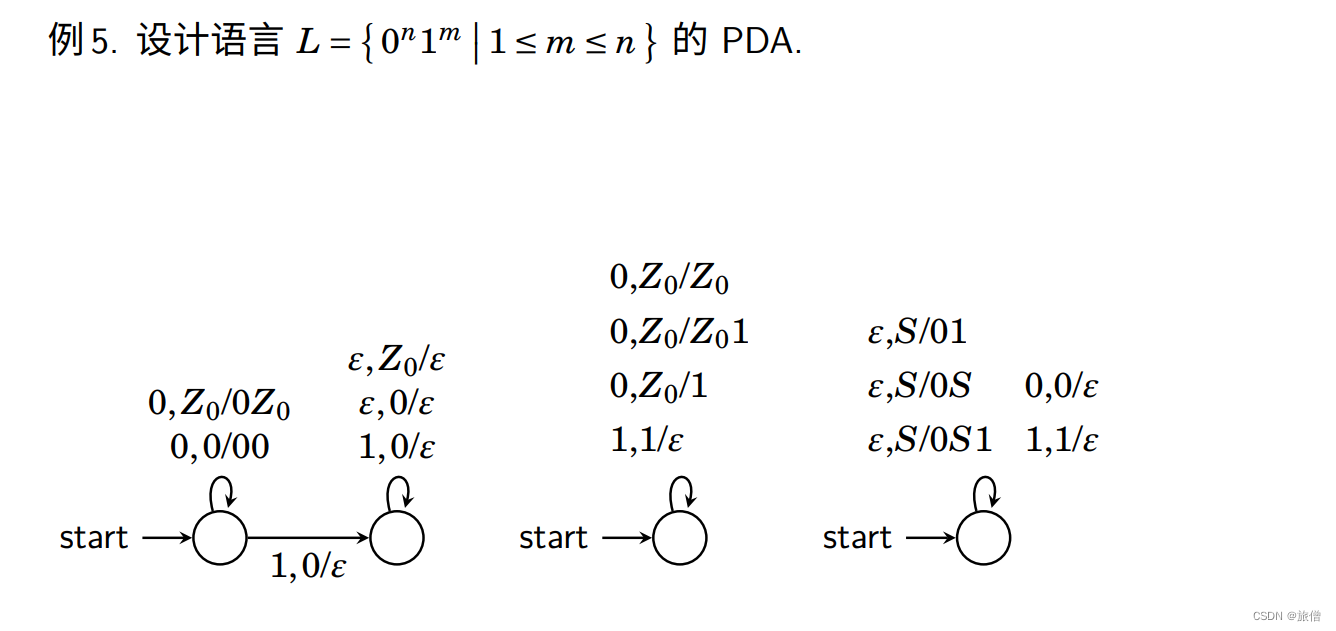
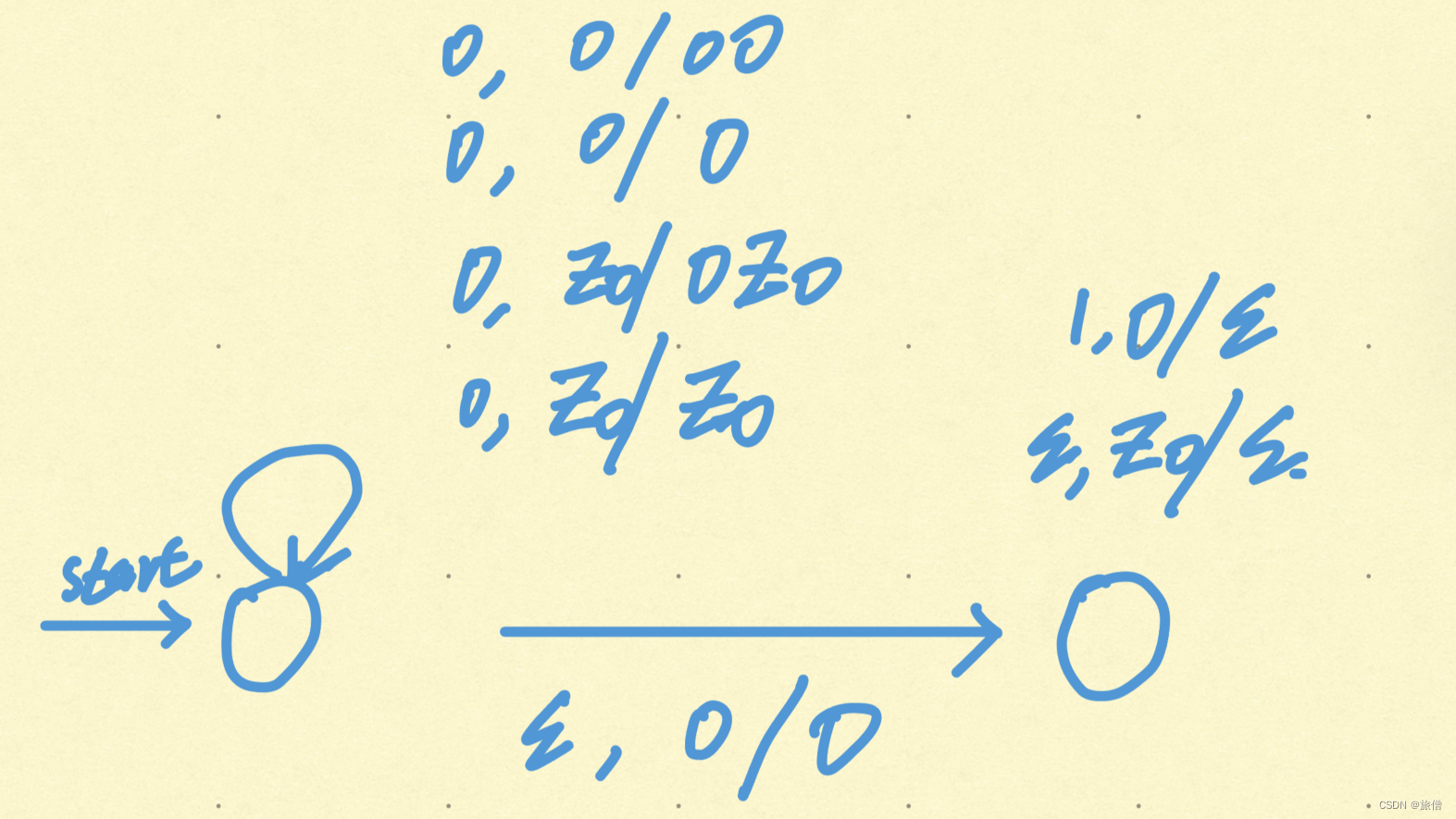

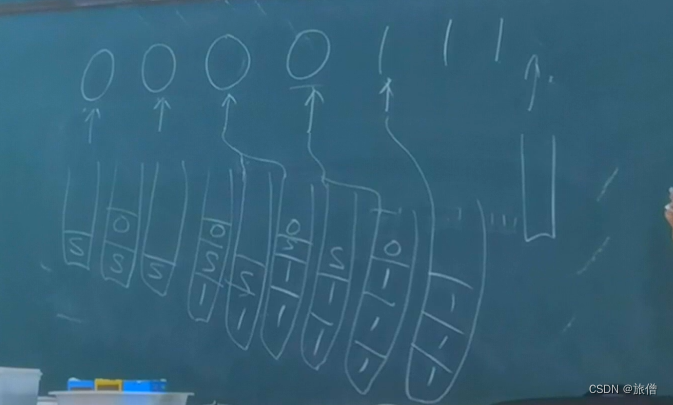
1.一部分来自规则2.一部分来自终止符号

举例1:对设计文法.

举例2:任何的PDA都可以通过文法转换过来
