一：离散余弦变换（Discrete Cosine Transform，DCT）

离散余弦变换（Discrete Cosine Transform，DCT）：是一种数学变换，它将一连串的离散值，如数字图像或信号，转换为代表图像或信号的频率成分的系数序列。DCT被广泛用于图像和信号处理、数据压缩和数字通信中。DCT的主要优点之一是它提供了一个图像或信号在其主要频率成分方面的紧凑表示，使其有可能在不损失很多信息的情况下压缩数据。DCT类似于更知名的傅里叶变换，但更适合于处理现实世界中具有有限长度和非周期性的信号和图像。DCT被用于几种流行的图像和视频压缩格式，如JPEG和MPEG

（1）一维DCT

A：定义

一维DCT变换定义：一维DCT是一种数学变换，它为一个给定的输入序列计算一组频率系数，使用不同频率的余弦函数的加权和。由此产生的频率系数可用于分析和压缩输入序列，以及其他应用。定义式如下

• $f(x)$代表输入信号或序列，它由**$N$样本或数值**组成
• DCT用于将这个输入序列转换为一组$N$的频率系数$F(u)$，其中$u$是频率系数的索引
• 求和里面的余弦函数是DCT的主要部分。它的参数由索引$u$和样本索引$x$组成，其参数由$\frac{(2x+1)u\pi }{2N}$给出。余弦函数用于提取输入序列的频率成分，而求和则用于计算每个样本对每个频率系数的贡献
• 因子$\sqrt{\frac{2}{N}}$是一个归一化常数，确保DCT是一个正交变换，也就是说，它保留了输入序列的能量。常数$C(u)$是另一个归一化常数，它取决于索引$u$和正在使用的DCT的变体。DCT的不同变体使用不同的归一化常数，这影响了变换的特性

$$F(u)=C(u)\sqrt{\frac{2}{N}}\sum _{x=0}^{N-1}f(x)\cos \frac{(2x+1)u\pi }{2N}u=0,1,\cdots ,N-1$$

一维IDCT变换定义：IDCT是DCT的逆变换，定义式如下

$$f(x)=\sqrt{\frac{2}{N}}\sum _{u=0}^{N-1}C(u)F(u)\cos \frac{(2x+1)u\pi }{2N}x=0,1,\cdots ,N-1$$

其中$C(u)=\{\begin{array}{lc}\frac{1}{\sqrt{2}}& u=0\\ 1& u=1,2,\dots ,N-1\end{array}$

B：实例

如下，有一长为4的数组序列，求其DFT

$$F(u)=C(u)\sqrt{\frac{2}{4}}\sum _{x=0}^{3}f(x)\cos \frac{(2x+1)u\pi }{8}u=0,1,2,3$$

如下

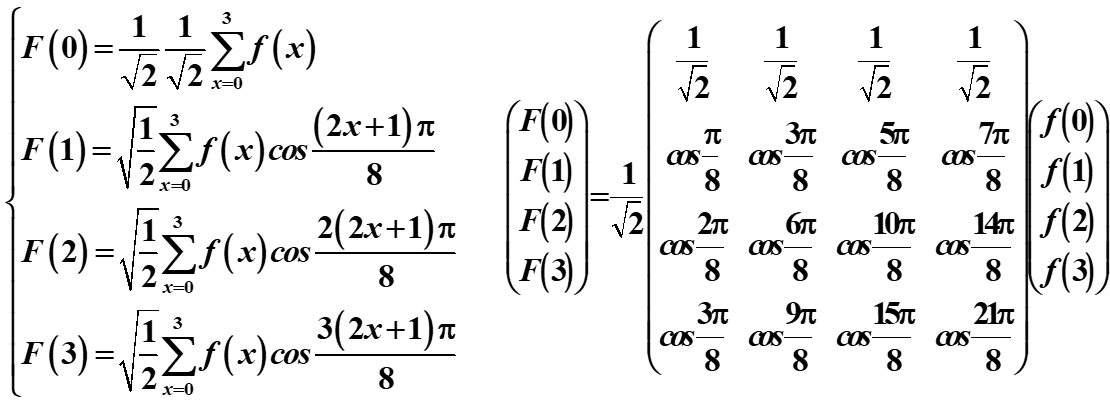
矩阵形式如下

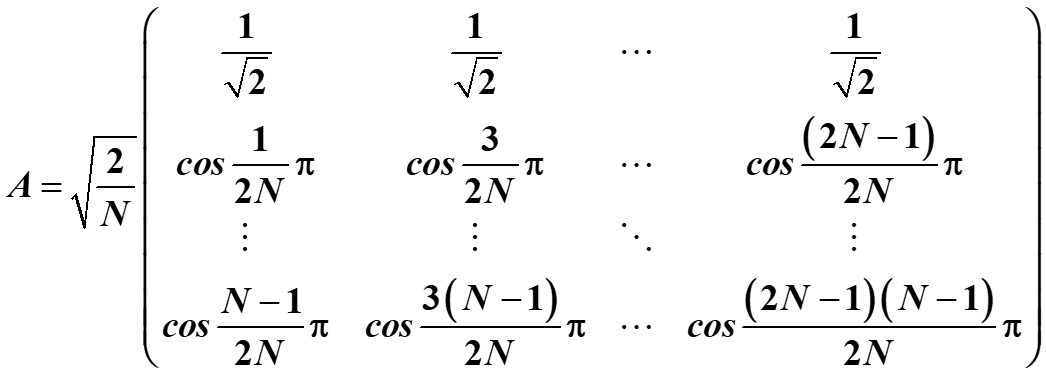
（2）二维DCT

A：定义

二维DCT变换与逆变换定义：二维离散余弦变换（DCT）是一维DCT向二维的扩展。它用于将二维信号或图像转换为二维频域中的一组频率系数。总之，二维DCT是一种数学变换，它为给定的输入图像计算一组频率系数，使用具有不同水平和垂直频率的余弦函数的加权和。由此产生的频率系数可用于分析和压缩输入图像，以及其他应用

• $f(x,y)$代表输入图像，它由$M$行和$N$列的像素组成
• DCT用于将该输入图像转换为一组频率系数$F(u,v)$，其中$u$和$v$分别为水平和垂直方向上的频率系数的指数
• 二维DCT的方程式与一维DCT的方程式相似，但在二维输入图像上有一个额外的求和。求和中的余弦函数由指数$u$、$v$、$x$和$y$设置参数，其参数分别由$\frac{\pi (2x+1)u}{2M}$ 和 $\frac{\pi (2y+1)v}{2N}$给出。余弦函数被用来提取输入图像的水平和垂直频率分量，并通过求和来计算每个像素对每个频率系数的贡献
• 因子$\frac{2}{\sqrt{MN}}$、$C(u)$和$C(v)$是归一化常数，确保DCT是一种正交变换，输入图像的能量被保留下来。这些常数取决于指数$u$、$v$和正在使用的DCT的变体

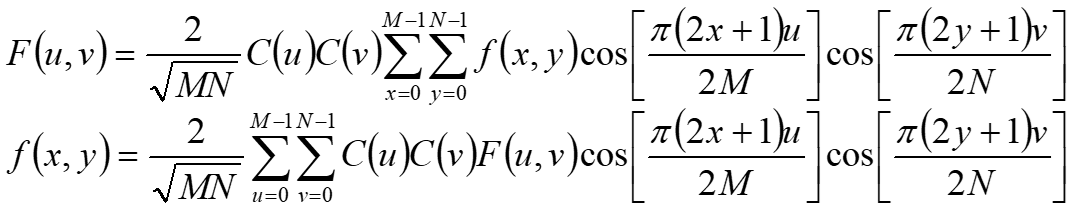
其中

$$\begin{array}{c}x,u=0,1,2,\cdots ,M-1\\ y,v=0,1,2,\cdots ,N-1\\ C(u),C(v)=\{\begin{array}{ll}\frac{1}{\sqrt{2}}& u,v=0\\ 1& u,v=1,2,\dots ,N-1\end{array}\end{array}$$

二维DCT变换的矩阵形式表示为

$$F=Af{A}^T,f=A^{T}FA$$

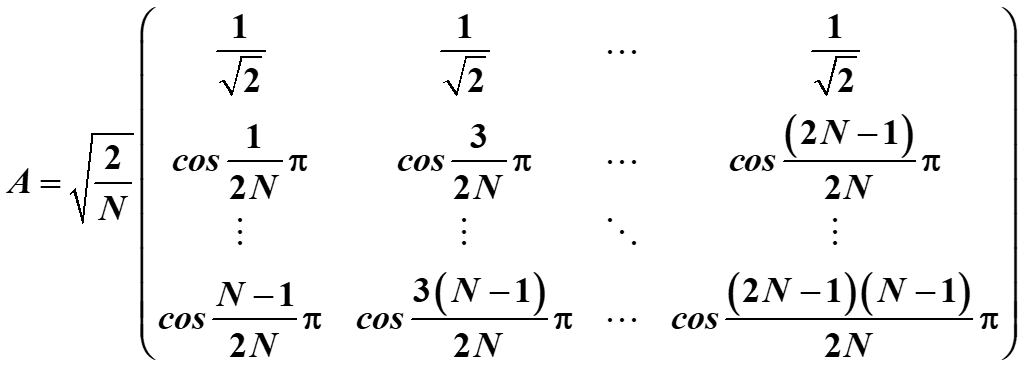
B：实例

如下有一幅输入图像$f(x,y)$，使用矩阵算法求其DCT

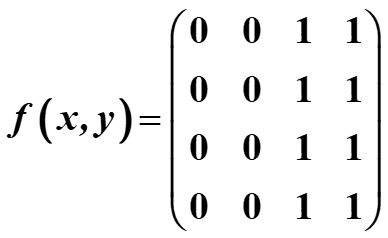
如下

C：程序

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册

• dct：这个函数计算给定输入信号或序列的一维离散余弦变换（DCT）。DCT用于将输入信号转换为频域中的一组频率系数。DCT函数需要以下参数
  • Src：输入信号或序列
  • dst：输出频率系数
  • flags：一组控制DCT行为的标志
  • nonzeroRows：输入信号中非零行的数量（可选）
• idct：该函数计算一组给定频率系数的一维离散余弦逆变换（IDCT）。IDCT用于将频率系数转换回原始信号或序列。idct函数接收以下参数
  • src：输入频率系数
  • dst：输出信号或序列
  • flags：一组控制IDCT行为的标志
  • nonzeroRows：输入频率系数中非零行的数量（可选）
• dct2：该函数计算给定输入图像的二维离散余弦变换（DCT）。DCT用于将输入图像转换为二维频域中的一组频率系数。dct2函数接受以下参数
  • src：输入图像
  • dst：输出频率系数
  • flags：一组控制DCT行为的标志
  • nonzeroRows：输入图像中非零行的数量（可选）
  • nonzeroCols：输入图像中非零列的数量（可选）
• idct2：这个函数计算一组给定频率系数的二维离散余弦逆变换（IDCT）。IDCT用于将频率系数转换回原始图像。idct2函数接受以下参数
  • src：输入频率系数
  • dst：输出图像
  • flags：一组控制IDCT行为的标志
  • nonzeroRows：输入频率系数中非零行的数量（可选）
  • nonzeroCols：输入频率系数中非零列的数量（可选）

实现如下效果

Image=imread('cameraman.jpg');%读取图像
imshow(Image);%显示原图像
grayI=rgb2gray(Image);%将彩色图像灰度化
figure,imshow(grayI);
DCTI=dct2(grayI);%计算余弦变换并移位
ADCTI=abs(DCTI);
top=max(ADCTI(:));
bottom=min(ADCTI(:));
ADCTI=(ADCTI-bottom)/(top-bottom)*100;
figure,imshow(ADCTI);%显示余弦变换频谱图
imwrite(ADCTI,'cameramandct.jpg');

Python实现：使用Python实现上述同样的功能

• cv2.dct：DCT
• cv2.idct：IDCT

import cv2
import numpy as np
from matplotlib import pyplot as plt

# 读取图像
Image = cv2.imread('cameraman.jpg')

# 显示原图像
cv2.imshow('Original Image', Image)
cv2.waitKey(0)

# 将彩色图像灰度化
grayI = cv2.cvtColor(Image, cv2.COLOR_BGR2GRAY)

# 显示灰度图像
cv2.imshow('Grayscale Image', grayI)
cv2.waitKey(0)

# 计算离散余弦变换
DCTI = cv2.dct(np.float32(grayI))

# 计算幅值并将其归一化到0-100之间
ADCTI = cv2.convertScaleAbs(DCTI)
ADCTI = cv2.normalize(ADCTI, None, 0, 100, cv2.NORM_MINMAX)

# 显示余弦变换频谱图
plt.imshow(ADCTI, cmap='gray')
plt.show()

# 保存离散余弦变换频谱图
cv2.imwrite('cameramandct.jpg', ADCTI)

（3）DCT在图像处理中的应用

DCT在图像处理中的应用：

• 图像压缩：DCT常用于图像压缩中，它基于图像的统计特征，将图像数据压缩到更少的存储空间中，而且在重建过程中，可以几乎无损地还原原始图像
• 图像水印：DCT可以用于图像水印的嵌入、提取和检测。通过将图像做DCT变换，然后将水印数据嵌入到DCT域的系数值中，以实现图像水印功能
• 图像特征提取：DCT可以用于图像的特征提取，在图像分类、图像识别、目标追踪等领域中有广泛的应用。在DCT域中，最大的系数值通常表示最明亮、最精细的细节，因此可以用于提取图像的特征
• 图像去噪：噪声常常会影响图像的质量和信息，DCT可以用于去除图像的高频噪声，以及平滑图像的细节信息，从而实现图像去噪的目的

二：K-L变换（Karhunen-Loeve Transform）