矩阵特征值与特征向量的理解
各位朋友大家好,我是小C哈哈哈,很高兴认识大家,在这里,我会将一些枯燥难懂的数学和算法知识以图片或动画的形式通俗易懂的展现给大家,希望大家喜欢。
线性代数中的矩阵特征值与特征向量这两个基本概念总是让很多人摸不着头脑,😄数学还是一如既往的晦涩难懂(ps: 放过我吧!)🍗。今天我们就以通俗的语言来讲解一下它们到底是什么?
在讲解矩阵特征值与特征向量之前,我们先来介绍一下几个基本的概念🌏。
映射🏠:指的是自变量集合到因变量集合的相互"对应关系"。
矩阵可以完成一个向量空间到另一个向量空间的映射,怎么理解呢?看下图,某向量x1经过矩阵A映射后变成了Ax1,某向量x2,经过矩阵A映射后变成了Ax2。
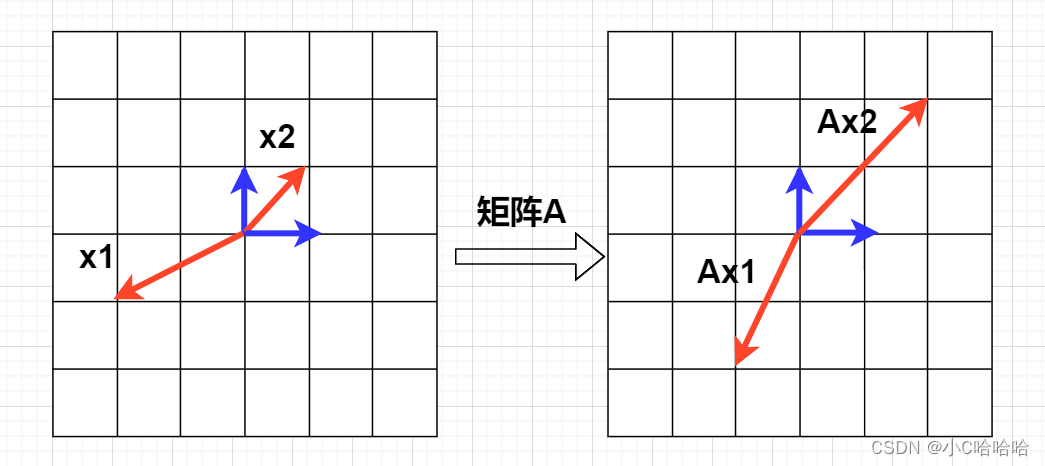
在上图中,映射前的x1与其对应的映射后的向量Ax1不在一条直线上,而映射前的x2与其对应的映射后的向量Ax2在同一条直线上,这种映射前后在同一条指向上的向量,就称为特征向量。
且这里的矩阵A对x2只起到了伸缩作用 ,那么Ax2就可以表示为λx2,这里的λ就称为矩阵A的特征值,x2称为此特征值对应的特征向量。
也就是说,非零向量x满足Ax = λx,那么λ就称为矩阵A的特征值,x称为矩阵A对应于特征值λ的特征向量。
