SVM原理理解
目录
概念推导:
共识:距离两个点集距离最大的分类直线的泛化能力更好,更能适应复杂数据。
怎么能让margin最大?
最大化margin即:
拉格朗日乘子法:
为什么公式中出现求和符号?
SVM模型:
小结:
学习资料:
猫都能看懂的SVM【从概念理解、优化方法到代码实现】_哔哩哔哩_bilibili
不简单的SVM - 知乎 (zhihu.com)
机器学习中的超平面wx+b=0?_平面方程wx+b=0-CSDN博客
优化-拉格朗日乘子法 - 知乎 (zhihu.com)
概念推导:
样本集:
类别标签:
分类直线:
当时,表示点在分类直线上;
表示该点在直线上方,表示该点为正样本;
表示该点在直线下方,该点为负样本;将上述转化为数学语言,即:
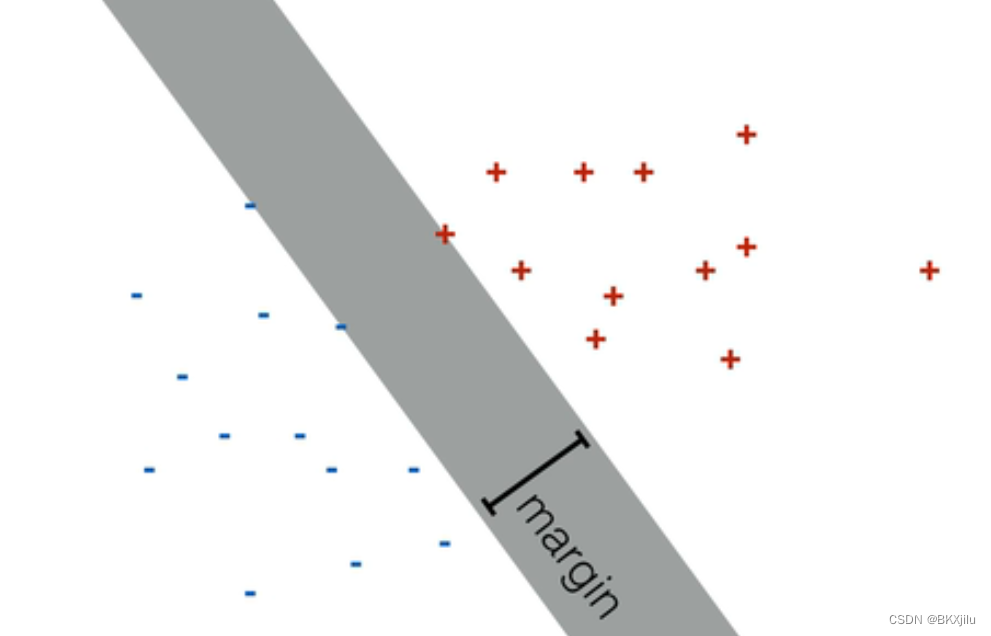
对于二分类问题,我们可以找到许多分类直线将不同点集正确区分。如下图:灰色面中的直线都是分类直线。margin表示间隔。
共识:距离两个点集距离最大的分类直线的泛化能力更好,更能适应复杂数据。
因此我们希望所有的点都被正确分类并且落在两条直线的两侧,且直线内区域尽量大。对上述公式进行改进:即在(-1,1)时,不分类
怎么能让margin最大?
计算最大间隔:,
表示分类直线边界上里最佳分类直线距离最近的两点;最大间隔margin为
,
之间的距离,等于
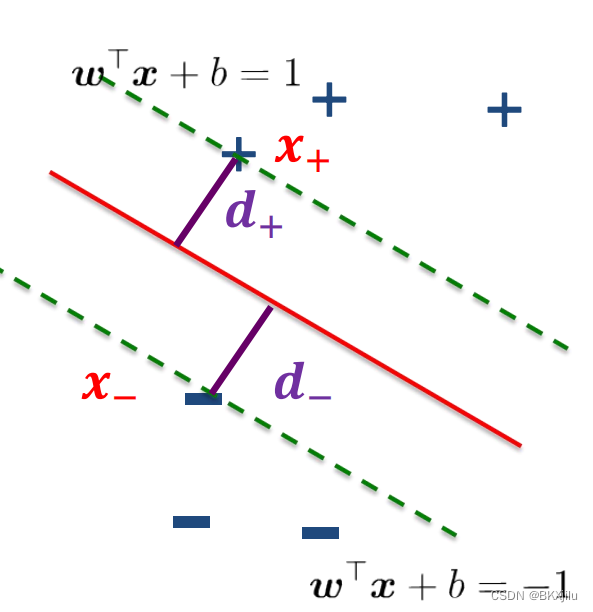
由直线外一点到直线的距离:直线:
(二维平面上公式:ax+by+c=0 点坐标为(x,y),二分类散点图上点坐标为(x1,x2)表示不同特征
w和x是矩阵 wx+b=w1x1+w2x2+b。所以直线上点满足w1x1+w2x2+b=0,
机器学习中的超平面wx+b=0?_平面方程wx+b=0-CSDN博客)
得:
又:
得:
最大化margin即:
,
,
求最小值,需要对
求偏导数,令其等于0,得到可能的极值点
对其求偏导(可以看成w可以看成(w1,w2,w3,,,wn),对求偏导是多元函数求偏导,对wi求偏导)
故:
,
问题转化:求条件下,
的极值->寻找多元函数不等式约束下的极值
拉格朗日乘子法:
优化-拉格朗日乘子法 - 知乎 (zhihu.com)
拉格朗日乘子法(Lagrange multipliers)是一种寻找多元函数在一组约束下的极值的方法。
通过引入拉格朗日乘子,可将有 d个变量与 k 个约束条件的最优化问题转化为具有 d+k个变量的无约束优化问题求解。
即:求f(x)在g(x)<=0的极值点。转化为:求L(x,u)=f(x)+ug(x)(u表示为拉格朗日乘子)的极值点。
求L(x,u)极值点的条件:(KKT条件)
求条件下,
的极值,数学语言表示:
为什么公式中出现求和符号?
L(x,u)=f(x)+ug(x)中:一个u对应一个x.
L(w,b,a)中w={w1,w2,,,wn},需要对应n个拉格朗日乘子。
KKT条件:
,
注意:对于不在两分类直线上的点(),
如图所示:

将,
带入.
得.
SVM模型:
小结:
1.Logistic算法和SVM的区别和联系:
模型不同:、
,Logistic模型更简单,SVM更复杂。
决策边界不同,都能解决分类问题:Logistic解决二分类问题,得到分类直线;SVM可以解决二分类,使用间隔最大化确定一个决策面。
